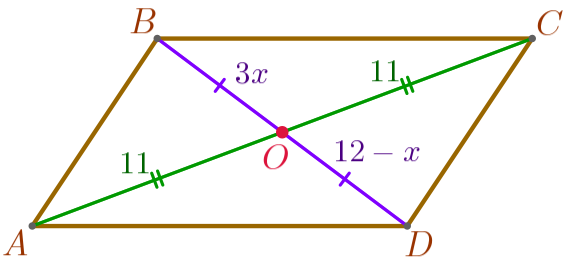
В четырёхугольнике \(\displaystyle ABCD\) диагонали \(\displaystyle AC\) и \(\displaystyle BD\) пересекаются в точке \(\displaystyle O{\small.}\) Известно, что \(\displaystyle AO=11\, {\footnotesize см}{\small,}\) \(\displaystyle OC=11\, {\footnotesize см}{\small,}\) \(\displaystyle BO=3x\, {\footnotesize см}{\small,}\) \(\displaystyle OD=(12-x)\, {\footnotesize см}{\small.}\)
При каком значении \(\displaystyle x\) четырёхугольник \(\displaystyle ABCD\) будет параллелограммом?
\(\displaystyle x=\)
Признак параллелограмма
 | Если диагонали четырёхугольника делятся точкой пересечения пополам, то он является параллелограммом. |
Согласно признаку четырёхугольник, \(\displaystyle ABCD\) будет параллелограммом, если точка \(\displaystyle O\) будет серединой диагонали \(\displaystyle AC\) и диагонали \(\displaystyle BD{\small.}\)
В четырёхугольнике \(\displaystyle ABCD{\small:}\)
|  |
Так как \(\displaystyle AO=OC{\small,}\) то точка \(\displaystyle O\) – середина диагонали \(\displaystyle AC{\small.}\)
То есть будет выполняться равенство:
\(\displaystyle BO=OD{\small.}\)
Подставим \(\displaystyle BO=3x\) и \(\displaystyle OD=12-x{\small:}\)
\(\displaystyle 3x=12-x{\small;} \)
\(\displaystyle 4x=12{\small;} \)
\(\displaystyle x=3{\small.} \)
Значит, диагонали \(\displaystyle AC\) и \(\displaystyle BD\) делятся точкой пересечения пополам при \(\displaystyle x=3{\small.}\)
Следовательно, при \(\displaystyle x=3\) четырёхугольник \(\displaystyle ABCD\) является параллелограммом.
Ответ: \(\displaystyle x=3{\small.}\)