В четырёхугольнике \(\displaystyle ABCD\) длины двух сторон равны \(\displaystyle 5\, {\footnotesize см}{\small,}\) а длины двух других сторон – \(\displaystyle 4\, {\footnotesize см}{\small.}\)
Является ли четырёхугольник \(\displaystyle ABCD\) параллелограммом?
Почему?
Признак параллелограмма
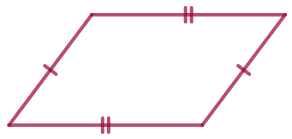 | Если у четырёхугольника противоположные стороны попарно равны, то он является параллелограммом. |
По условию задачи в четырёхугольнике \(\displaystyle ABCD\) стороны попарно равны, но не сказано, какие именно стороны равны.
Например, возможны такие варианты:
| \(\displaystyle 1.\) | 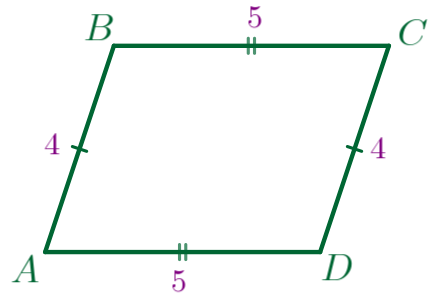 |
То есть противоположные стороны попарно равны: \(\displaystyle AB=CD{\small,}\) \(\displaystyle BC=AD{\small.}\) |
В этом случае четырёхугольник \(\displaystyle ABCD\) является параллелограммом. | ||
| ||
| \(\displaystyle 2.\) | 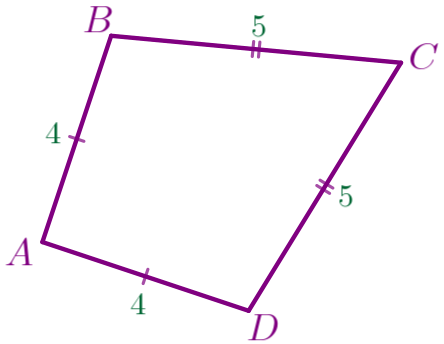 |
То есть противоположные стороны не равны: \(\displaystyle AB\, \cancel=\, CD{\small,}\) \(\displaystyle BC\, \cancel=\, AD{\small.}\) |
В этом случае четырёхугольник \(\displaystyle ABCD\) не является параллелограммом. | ||
Следовательно, в условии задачи недостаточно исходных данных для того, чтобы определить вид четырёхугольника \(\displaystyle ABCD{\small.}\)
| Ответ: | Является ли четырёхугольник \(\displaystyle ABCD\) параллелограммом? Невозможно определить. Почему? Недостаточно исходных данных. |