В выпуклом четырёхугольнике \(\displaystyle ABCD\) \(\displaystyle \angle A=60^{\circ}{\small,}\) \(\displaystyle \angle B=60^{\circ}{\small,}\) \(\displaystyle \angle C=120^{\circ}{\small.}\)
Является ли четырёхугольник \(\displaystyle ABCD\) параллелограммом?
Почему?
Признак параллелограмма
Если у четырёхугольника противоположные углы попарно равны, то он является параллелограммом. | 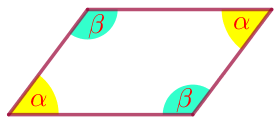 |
В выпуклом четырёхугольнике \(\displaystyle ABCD\) противоположные углы \(\displaystyle \color{Orangered}{A}\) и \(\displaystyle \color{green}{C}\) не равны.
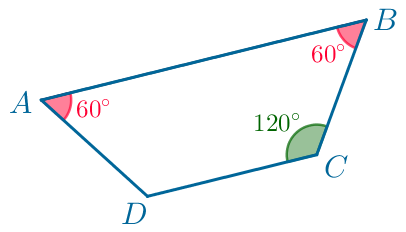 | \(\displaystyle \color{Orangered}{\angle A}=\color{Orangered}{60^{\circ}}{\small,}\) \(\displaystyle \color{green}{\angle C}=\color{green}{120^{\circ}}{\small.}\) |
Следовательно,
\(\displaystyle ABCD\) не является параллелограммом.
| Ответ: | Является ли четырёхугольник \(\displaystyle ABCD\) параллелограммом? Нет. Почему? Противоположные углы не равны. |