В равнобедренной трапеции \(\displaystyle KLMN\) угол \(\displaystyle K\) равен \(\displaystyle 56^{\circ}{\small.}\) Найдите угол \(\displaystyle M{\small.}\)
\(\displaystyle \angle M=\)\(\displaystyle ^{\circ}{\small.}\)
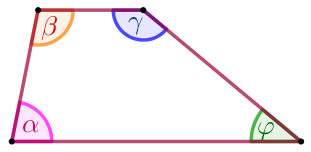
\(\displaystyle KLMN\) – равнобедренная трапеция:
Требуется найти угол \(\displaystyle M{\small.}\) | 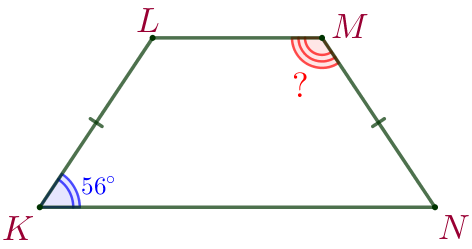 |
| Углы при основании равнобедренной трапеции равны. | 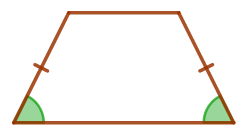 |
Согласно свойству в трапеции \(\displaystyle KLMN{\small:}\)
| 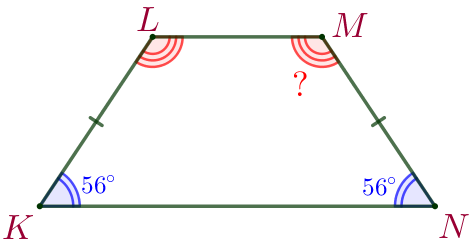 |
\(\displaystyle \color{blue}{\angle {N}}+\color{red}{\angle M}= 180^{\circ}{\small.}\)
Получаем
\(\displaystyle \color{red}{\angle M}= 180^{\circ}-\color{blue}{\angle {N}}= 180^{\circ}-56^{\circ}= 124^{\circ}{\small.}\)
Ответ: \(\displaystyle \angle M=124^{\circ} {\small.}\)