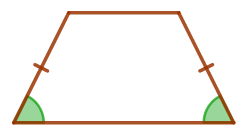
Основания равнобедренной трапеции равны \(\displaystyle 21\) и \(\displaystyle 5{\small,}\) высота равна \(\displaystyle 8{\small.}\) Найдите острый угол трапеции. Ответ дайте в градусах.
\(\displaystyle ^{\circ}\)
Пусть \(\displaystyle ABCD\) – равнобедренная трапеция:
| 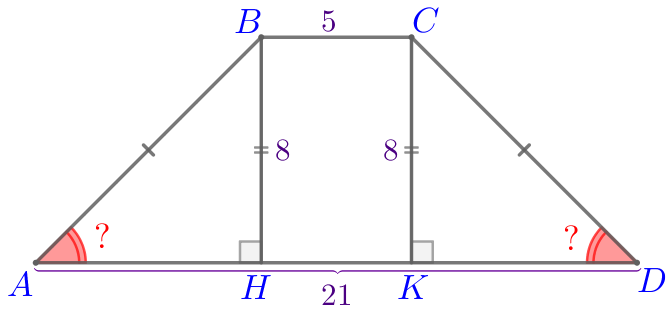 |
Требуется найти острый угол трапеции \(\displaystyle ABCD{\small:}\)
\(\displaystyle \angle A=\angle D=\color{red}{\large ?}\)
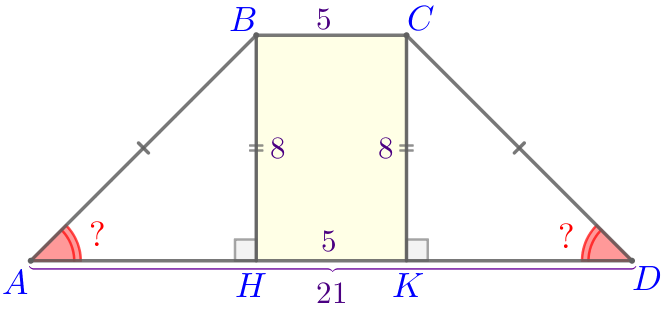 |
Следовательно, \(\displaystyle BCKH \) – прямоугольник. Тогда \(\displaystyle HK=BC=5{\small.}\) |
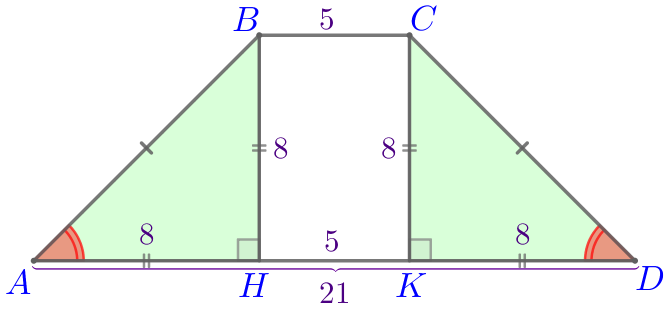 |
Следовательно, \(\displaystyle \triangle ABH= \triangle DCK\) по гипотенузе и катету. |
Значит,
\(\displaystyle AH=DK=\frac{AD-HK}{2}{\small;}\\ \)
\(\displaystyle AH=\frac{21-5}{2}=\frac{16}{2}=8{\small.}\)
Рассмотрим прямоугольный треугольник \(\displaystyle AHB{\small:}\) Так как \(\displaystyle BH=AH=8{\small,}\) то \(\displaystyle \triangle ABH\) – равнобедренный. По свойству равнобедренного треугольника \(\displaystyle \angle HAB=\angle HBA{\small.}\) | 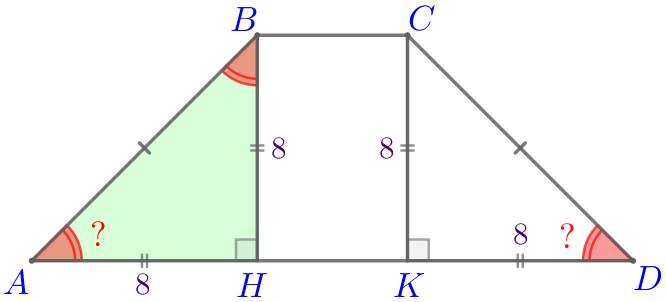 |
Сумма острых углов прямоугольного треугольника равна \(\displaystyle 90^{\circ}{\small.}\) Значит,
\(\displaystyle \angle HAB+\angle HBA=90^{\circ}{\small,}\)
\(\displaystyle 2 \cdot \angle HAB=90^{\circ}{\small,}\)
\(\displaystyle \angle HAB=90^{\circ}:2=45^{\circ}{\small.}\)
Острый угол трапеции \(\displaystyle ABCD\) равен \(\displaystyle 45^{\circ}{\small.}\)
Ответ: \(\displaystyle 45^{\circ}{\small.}\)