Теория: Углы

Задание

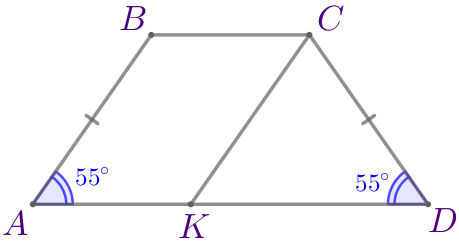
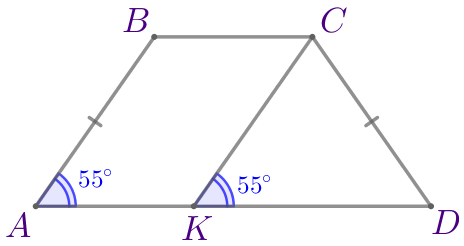
В равнобедренной трапеции \(\displaystyle ABCD\) на основании \(\displaystyle AD\) отметили точку \(\displaystyle K\) так, что прямая \(\displaystyle CK\) параллельна \(\displaystyle AB{\small.}\) Найдите угол \(\displaystyle KCD {\small,}\) если \(\displaystyle \angle A=55^{\circ}{\small.}\) Ответ дайте в градусах.

\(\displaystyle \angle KCD=\)\(\displaystyle ^{\circ}{\small.}\)

Решение

\(\displaystyle ABCD\) – равнобедренная трапеция:

\(\displaystyle AB=CD{\small;}\)
\(\displaystyle CK \parallel AB{\small;}\)
\(\displaystyle \angle A=55^{\circ}{\small.}\)

Требуется найти угол \(\displaystyle KCD{\small.}\)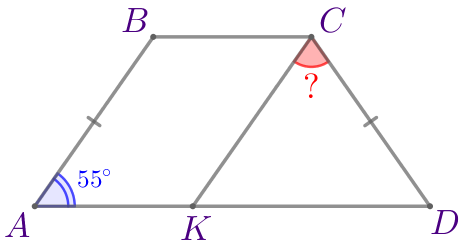

Свойство равнобедренной трапеции

Углы при основании равнобедренной трапеции равны.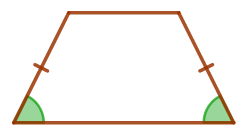

\(\displaystyle \angle A=\angle D=55^{\circ}{\small.}\)

\(\displaystyle \angle CKD= \angle BAD=55^{\circ}{\small.}\)

Рассмотрим треугольник \(\displaystyle KCD{\small.}\)

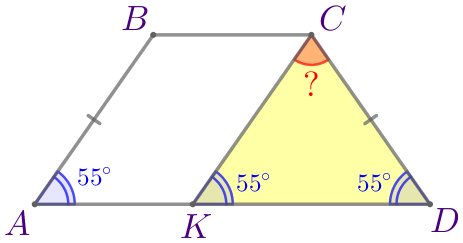Сумма внутренних углов треугольника равна \(\displaystyle 180^{\circ}{\small,}\) значит,

\(\displaystyle \angle KCD=180^{\circ}-(\angle CKD + \angle CDK){\small;}\)

\(\displaystyle \angle KCD=180^{\circ}-(55^{\circ} + 55^{\circ}){\small;}\)

\(\displaystyle \angle KCD=180^{\circ}-110^{\circ}=70^{\circ}{\small.}\)

Ответ: \(\displaystyle \angle KCD=70^{\circ}{ \small.}\)