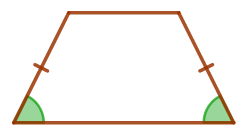
В равнобедренной трапеции \(\displaystyle ABCD\) с основаниями \(\displaystyle AD\) и \(\displaystyle BC\) угол \(\displaystyle CAD\) равен \(\displaystyle 36^{\circ }{\small,}\) \(\displaystyle O\) – точка пересечения диагоналей. Найдите угол \(\displaystyle AOD{\small.}\) Ответ дайте в градусах.
\(\displaystyle \angle AOD=\)\(\displaystyle ^{\circ}{\small.}\)
\(\displaystyle ABCD\) – равнобедренная трапеция:
Требуется найти угол \(\displaystyle AOD{\small.}\) | 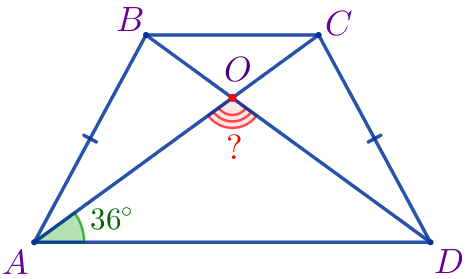 |
\(\displaystyle \angle CDA=\angle BAD{\small.}\)
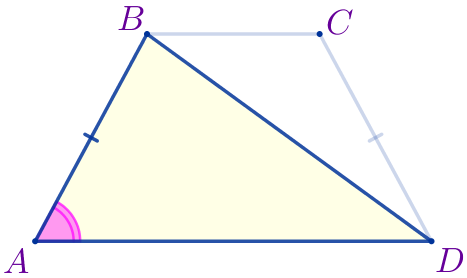 | 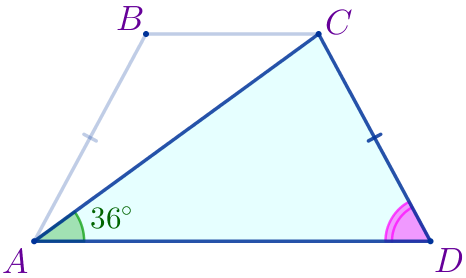 |
| |
Следовательно,
\(\displaystyle \triangle BAD=\triangle CDA\) – по двум сторонам и углу между ними.
Значит, углы \(\displaystyle BDA\) и \(\displaystyle CAD\) равны:
\(\displaystyle \angle BDA=\angle CAD=\color{green}{{36}^{\circ}}{\small.}\)
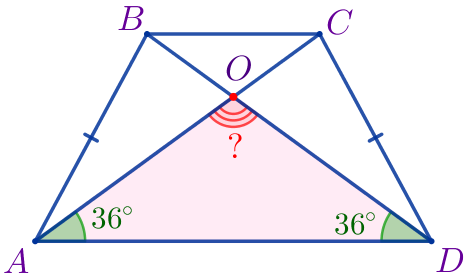 | Сумма внутренних углов треугольника равна \(\displaystyle 180^{\circ}{\small.}\) Тогда \(\displaystyle \angle AOD=180^{\circ} - ({\angle OAD} +{\angle ODA}){\small.}\) Подставим известные величины углов: \(\displaystyle \angle AOD=180^{\circ} - (\color{green}{36^{\circ}} + \color{green}{36^{\circ}} )=180^{\circ}-72^{\circ}=108^{\circ}{\small.} \) |
Ответ: \(\displaystyle \angle AOD=108^{\circ}{ \small.}\)