Сумма двух углов при основании равнобедренной трапеции равна \(\displaystyle 148^\circ\small.\) Найдите величину бóльшего угла трапеции. Ответ дайте в градусах.
\(\displaystyle ^{\circ}\)
Пусть \(\displaystyle ABCD\) – равнобедренная трапеция с основаниями \(\displaystyle AD\) и \(\displaystyle BC\small.\)
| Углы при основании равнобедренной трапеции равны. | 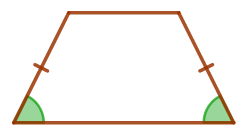 |
Согласно свойству в трапеции \(\displaystyle ABCD{\small:}\) \(\displaystyle \angle A=\angle D{\small,}\) \(\displaystyle \angle B=\angle C{\small.}\) | 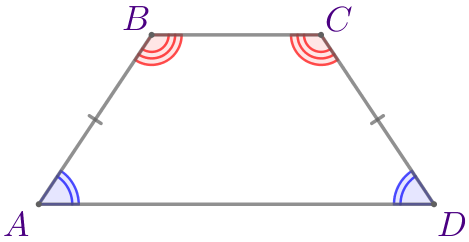 |
\(\displaystyle \angle A+\angle D=148^{\circ}{\small.}\)
Получаем:
\(\displaystyle 2\angle A=148^{\circ}{\small,}\)
\(\displaystyle \angle A=74^{\circ}{\small.}\)
\(\displaystyle {\angle {A}}+{\angle B}= 180^{\circ}{\small.}\)
\(\displaystyle \angle B=180^{\circ}-\angle A=180^{\circ}-74^{\circ}=106^{\circ}{\small.}\)
Бóльший угол трапеции равен \(\displaystyle 106^{\circ}{\small.}\)
Ответ: \(\displaystyle 106^{\circ}{\small.}\)