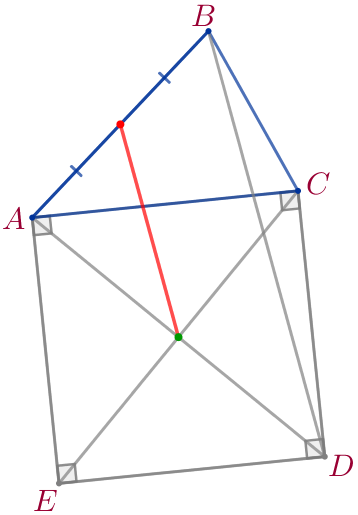
На стороне \(\displaystyle AC\) треугольника \(\displaystyle ABC\) построен квадрат \(\displaystyle ACDE{\small.}\) Найдите расстояние от середины стороны \(\displaystyle AB\) до точки пересечения диагоналей квадрата \(\displaystyle ACDE{\small,}\) если расстояние между точками \(\displaystyle B\) и \(\displaystyle D\) равно \(\displaystyle 18{\small.}\)
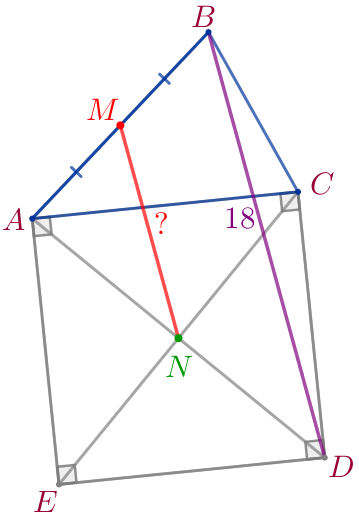 |
Требуется найти длину отрезка \(\displaystyle MN{\small.}\) |
Диагонали квадрата точкой пересечения делятся пополам, то есть \(\displaystyle N\) – середина \(\displaystyle AD{\small.}\)
Рассмотрим треугольник \(\displaystyle ABD{\small.}\)
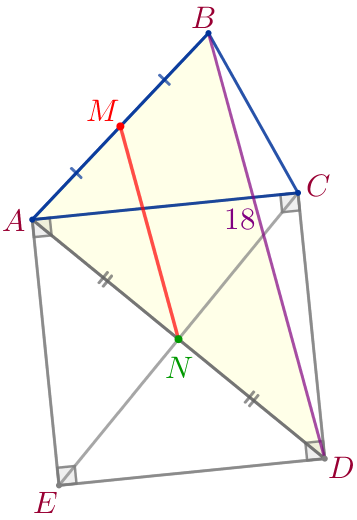
\(\displaystyle MN=\frac{1}{2} \cdot BD=\frac{1}{2} \cdot 18=9{\small.}\)
Ответ: \(\displaystyle 9{\small.}\)

