Прямая, параллельная стороне \(\displaystyle AC\) треугольника \(\displaystyle ABC{\small,}\) пересекает стороны \(\displaystyle AB\) и \(\displaystyle BC\) в точках \(\displaystyle M\) и \(\displaystyle N\) соответственно. Известно, что \(\displaystyle AC=8{\small,}\) \(\displaystyle BN=5{\small,}\) \(\displaystyle MN=4{\small.}\) Найдите \(\displaystyle BC{\small.}\)
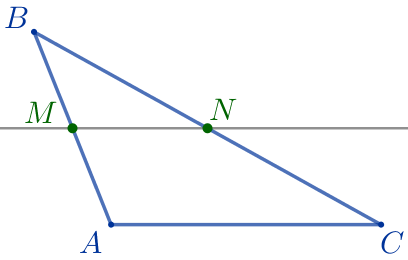
\(\displaystyle BC=\)
\(\displaystyle ABC\) – треугольник:
Прямая \(\displaystyle MN\) параллельна \(\displaystyle AC{\small.}\)
Требуется найти длину стороны \(\displaystyle BC{\small.}\) | 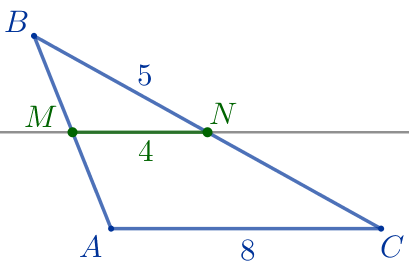 |
\(\displaystyle MN\) – средняя линия треугольника \(\displaystyle ABC{\small.}\)
Следовательно, точка \(\displaystyle N\) – середина стороны \(\displaystyle BC{\small.}\) Значит,
\(\displaystyle BC=2 \cdot BN{\small;}\)
\(\displaystyle BC=2 \cdot 5=10{\small.}\)
Ответ: \(\displaystyle BC=10{\small.}\)
