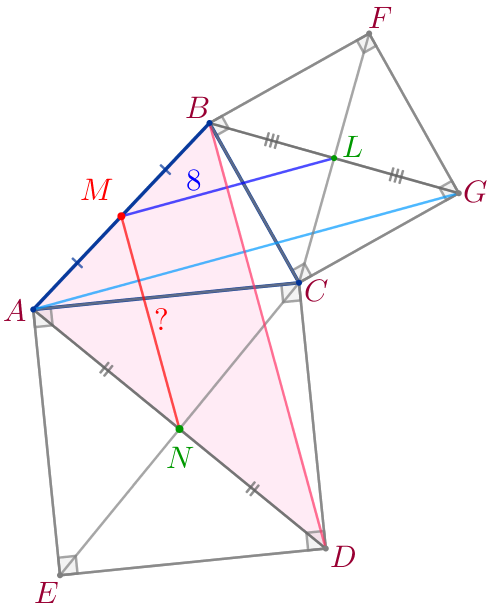
На сторонах \(\displaystyle AC\) и \(\displaystyle BC\) треугольника \(\displaystyle ABC\) построены квадраты \(\displaystyle ACDE\) и \(\displaystyle BCGF\) соответственно. Найдите расстояние от середины стороны \(\displaystyle AB\) до точки пересечения диагоналей квадрата \(\displaystyle ACDE{\small,}\) если расстояние от середины стороны \(\displaystyle AB\) до точки пересечения диагоналей второго квадрата равно \(\displaystyle 8{\small.}\)
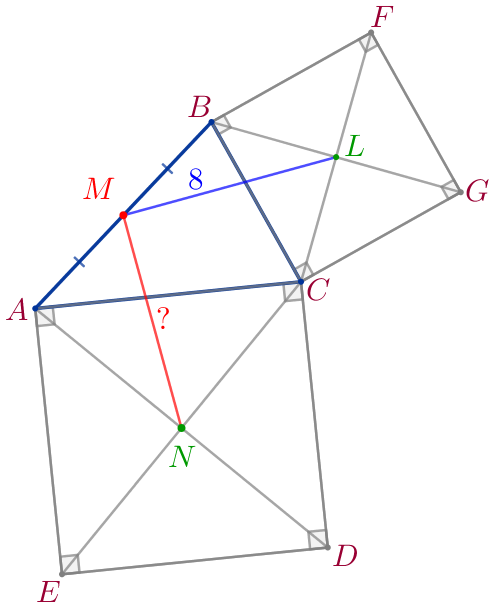 |
Требуется найти длину отрезка \(\displaystyle MN{\small.}\) |
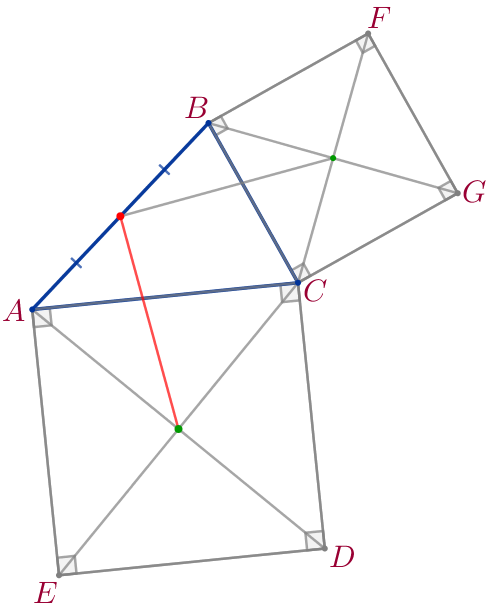
Выполним дополнительное построение.
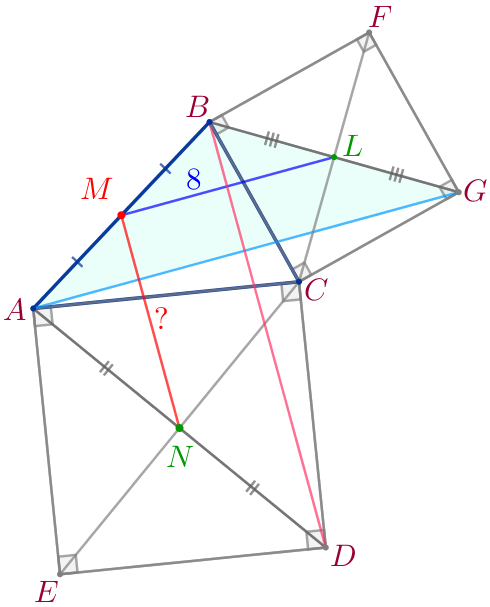
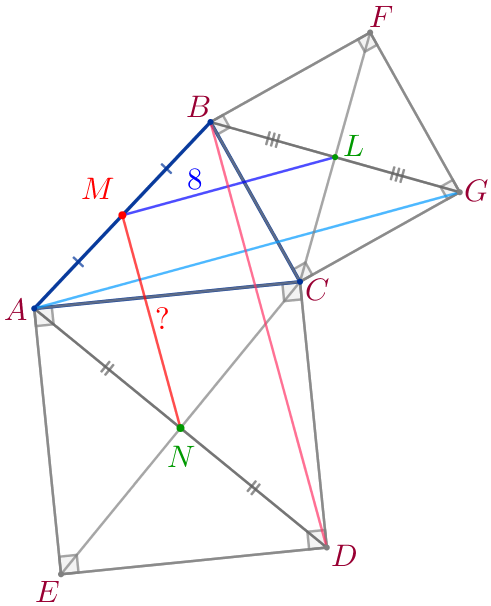 | Проведём отрезки \(\displaystyle BD\) и \(\displaystyle AG{\small.}\)
Диагонали квадрата точкой пересечения делятся пополам, значит,
\(\displaystyle AN=ND{\small;}\)
\(\displaystyle BL=LG{\small.}\) |
\(\displaystyle MN=\frac{1}{2} \cdot BD{\small.}\)
\(\displaystyle AG=16{\small.}\)
\(\displaystyle BD=16{\small.}\)
Рассмотрим треугольники \(\displaystyle BCD\) и \(\displaystyle ACG{\small.}\)
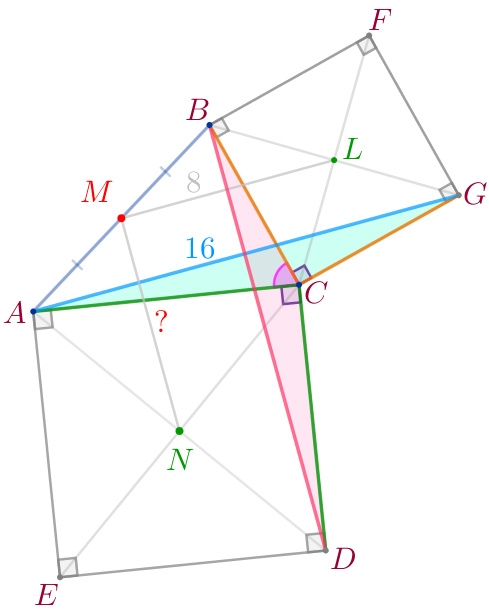 | Заметим, что \(\displaystyle \angle BCD=\angle ACB+\angle ACD=\angle ACB +90^{\circ}\) и \(\displaystyle \angle ACG=\angle ACB+\angle BCG=\angle ACB +90^{\circ}{\small,}\) значит, \(\displaystyle \angle BCD=\angle ACG{\small.}\)
Треугольники \(\displaystyle BCD\) и \(\displaystyle ACG\) равны по двум сторонам и углу между ними:
|
Следовательно,
\(\displaystyle BD=AG=16{\small.}\)
В результате получаем:
\(\displaystyle MN=\frac{1}{2} \cdot BD=\frac{1}{2} \cdot 16=8{\small.}\)
Ответ: \(\displaystyle 8{\small.}\)