Известна величина \(\displaystyle \alpha\) одного из углов, образовавшихся при пересечении двух прямых.
Дополните таблицу значений угла между прямыми в зависимости от значения \(\displaystyle \alpha{\small .}\)
| \(\displaystyle \alpha\) | Угол между прямыми \(\displaystyle p\) и \(\displaystyle q{\small .}\) |
| \(\displaystyle 87\degree \) | \(\displaystyle \degree \) |
| \(\displaystyle 90\degree \) | \(\displaystyle \degree \) |
| \(\displaystyle 92\degree \) | \(\displaystyle \degree \) |
| \(\displaystyle 89\degree 59'\) | \(\displaystyle \degree \)\(\displaystyle '\) |
| \(\displaystyle 90\degree 1'\) | \(\displaystyle \degree \)\(\displaystyle '\) |
При пересечении двух прямых образуется шесть углов с вершиной в их общей точке:
- два развёрнутых угла;
- две пары вертикальных углов, из которых можно также составить четыре пары смежных углов.

На рисунке две пересекающиеся прямые \(\displaystyle a\) и \(\displaystyle b{\small .}\)
Если выбрать любую пару вертикальных углов, то каждый угол другой пары будет смежным с каждым углом исходной.
Величину углов одной пары обозначим через \(\displaystyle \alpha{\small .}\) Тогда величина углов другой пары запишется как \(\displaystyle 180\degree -\alpha{\small .}\)
Угол между прямыми \(\displaystyle -\) та из этих двух величин, которая меньше или равна другой.
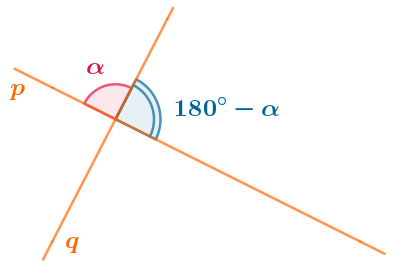
\(\displaystyle \alpha\) | \(\displaystyle 180\degree -\alpha\) | Угол между прямыми | |
| \(\displaystyle 87\degree \) | \(\displaystyle <\) | \(\displaystyle 180\degree -87\degree = 93\degree \) | \(\displaystyle 87\degree \) |
| \(\displaystyle 90\degree \) | \(\displaystyle =\) | \(\displaystyle 180\degree -90\degree = 90\degree \) | \(\displaystyle 90\degree \) |
| \(\displaystyle 92\degree \) | \(\displaystyle >\) | \(\displaystyle 180\degree -92\degree = 88\degree \) | \(\displaystyle 88\degree \) |
| \(\displaystyle 89\degree 59'\) | \(\displaystyle <\) | \(\displaystyle 180\degree -89\degree 59' = 90\degree 1'\) | \(\displaystyle 89\degree 59'\) |
| \(\displaystyle 90\degree 1'\) | \(\displaystyle >\) | \(\displaystyle 180\degree -90\degree 1' = 89\degree 59'\) | \(\displaystyle 89\degree 59'\) |
Для ответа на вопрос задачи в первом, втором и четвертом пунктах вычисления проделывать не обязательно.
В этих трёх случаях данная величина \(\displaystyle \alpha\) соответствует острому или прямому углу.
Значит, величина \(\displaystyle 180\degree -\alpha\) не меньше и в ответ можно сразу записывать значение \(\displaystyle \alpha{\small .}\)
| Ответ: |  |