Три прямые \(\displaystyle a{\small ,\;}b\) и \(\displaystyle c\) пересекаются в одной точке.
Угол между прямыми \(\displaystyle a\) и \(\displaystyle b\) равен \(\displaystyle 33\degree {\small .} \)
Угол между прямыми \(\displaystyle a\) и \(\displaystyle c\) равен \(\displaystyle 48\degree {\small .}\)
Какие значения может принимать угол между прямыми \(\displaystyle b\) и \(\displaystyle c{\text ?}\)
Сделаем соответствующий условиям задачи рисунок.
Обозначим на прямой \(\displaystyle a\) точку \(\displaystyle O~-\) общую точку трёх прямых.
Выберем
- один из лучей \(\displaystyle OA\) прямой \(\displaystyle a{\small ,}\)
- тот луч \(\displaystyle OB\) прямой \(\displaystyle b{ \small ,}\) который образует вместе с лучом \(\displaystyle OA\) угол, величина которого равна углу \(\displaystyle \beta=33\degree \) между прямыми \(\displaystyle a\) и \(\displaystyle b{\small .}\)
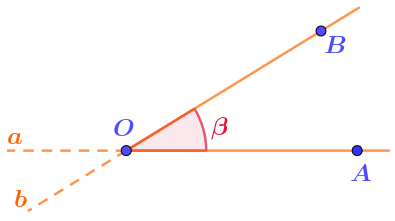
Это можно сделать двумя способами: луч \(\displaystyle OC\) может пройти с лучом \(\displaystyle OB\) по одну или по разные стороны прямой \(\displaystyle a{\small .}\)
В первом случае угол \(\displaystyle BOC\) будет частью угла \(\displaystyle AOC{\small ,\;}\) так как величина этого угла меньше величины \(\displaystyle \gamma=48\degree {\small .}\)
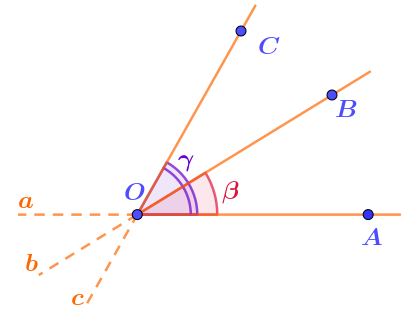
Тогда величина угла \(\displaystyle BOC\) равна:
\(\displaystyle \angle BOC=48\degree -33\degree =\)\(\displaystyle 15\degree {\small .}\)
Это величина одного из углов, образованных при пересечении прямых \(\displaystyle b\) и \(\displaystyle c{\small ,}\) и она меньше \(\displaystyle 90\degree {\small .}\)
То есть угол между прямыми \(\displaystyle b\) и \(\displaystyle c\)равен \(\displaystyle 15\degree {\small .}\)
Во втором случае углы \(\displaystyle AOB\) и \(\displaystyle AOC~-\) части угла \(\displaystyle BOC{\small ,}\) величина которого равна сумме их величин:
\(\displaystyle \angle BOC=48\degree +33\degree =\)\(\displaystyle 81\degree {\small .}\)
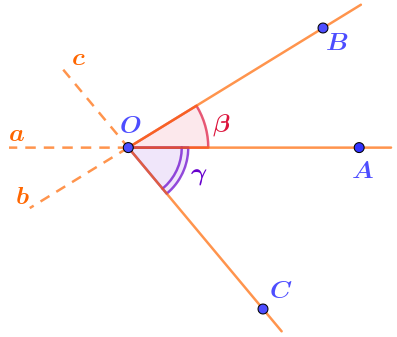
Это величина одного из углов, образованных при пересечении прямых \(\displaystyle b\) и \(\displaystyle c{\small ,}\) и она меньше \(\displaystyle 90\degree {\small .}\)
То есть угол между прямыми \(\displaystyle b\) и \(\displaystyle c\) равен \(\displaystyle 81\degree {\small .}\)
Ответ: \(\displaystyle 15\degree\) или \(\displaystyle 81\degree{\small .}\)