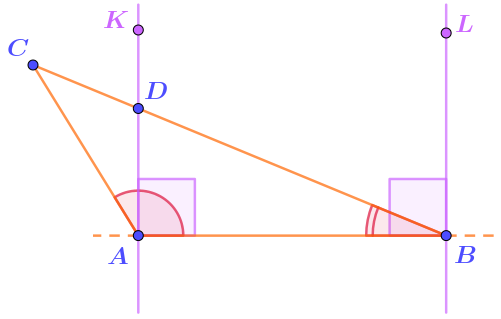
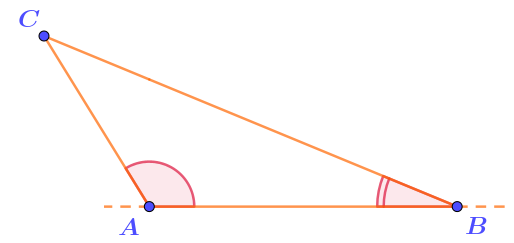
Первоначальные условия задачи описывают рисунок, на котором обозначены лишь точки \(\displaystyle A{ \small ,}\,B\) и \(\displaystyle C{\small .}\)
Первым фрагментом является тот, что описывает дополнительное построение. В остальных упоминаются точки, полученные при этом построении.
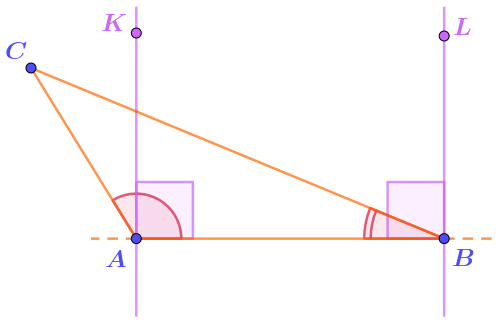
1. Проведём прямые, перпендикулярные прямой \(\displaystyle AB{\small ,}\) через точки \(\displaystyle A\) и \(\displaystyle B{\small .}\) Отметим на этих прямых соответственно точки \(\displaystyle K\) и \(\displaystyle L\) по ту сторону прямой \(\displaystyle AB{\small ,}\) где расположена точка \(\displaystyle C{\small .}\)
- Перпендикулярной к данной прямой называется прямая, образующая прямой угол с исходной.
- Через точку, принадлежащую прямой, можно провести прямую, перпендикулярную этой прямой, и только одну.
В нашем рассуждении мы пользуемся этой возможностью для того, чтобы сравнить рассматриваемые углы \(\displaystyle BAC\) и \(\displaystyle ABC\) с прямым углом.
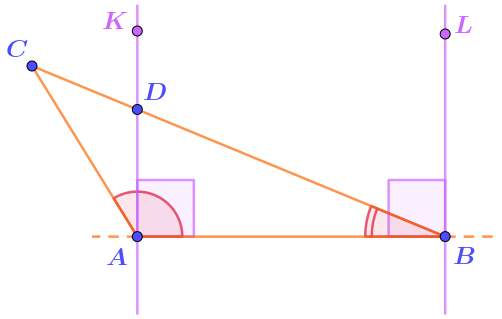
Чтобы получить важную для дальнейших рассуждений точку \(\displaystyle D{ \small ,}\) важно убедиться, что отрезок \(\displaystyle BC\) пересекает прямую \(\displaystyle AK{\small .}\)
Для этого подходит фрагмент, объясняющий, что точки \(\displaystyle B\) и \(\displaystyle C\) расположены по разные сторонвы прямой \(\displaystyle AK{\small .}\)
2. Угол \(\displaystyle BAC\) тупой. Значит, прямой угол \(\displaystyle BAK~-\) его часть. Следовательно, точки \(\displaystyle B\) и \(\displaystyle C\) расположены по разные стороны прямой \(\displaystyle AK{\small .}\)
Угол называется тупым, если его частью является прямой угол.
В нашем рассуждении от общей стороны \(\displaystyle AB\) отложены прямой угол \(\displaystyle BAK\) и тупой угол \(\displaystyle BAC{\small .}\) Поскольку отложены они в одну сторону от прямой \(\displaystyle AB{\small ,}\) первый должен стать частью второго.
Значит, луч \(\displaystyle AK\) проходит во внутренней области угла \(\displaystyle BAC{\small .}\) Иными словами, лучи \(\displaystyle AB\) и \(\displaystyle AC\) проходят по разные стороны прямой \(\displaystyle AK{\small .}\) Значит, и их точки \(\displaystyle B\) и \(\displaystyle C\) расположены по разные её стороны.
Далее, очевидно, необходим фрагмент, вводящий в рассмотрение точку \(\displaystyle D{\small .}\)
3. Значит, отрезок \(\displaystyle BC\) пересекает прямую \(\displaystyle AK\) в некоторой точке. Обозначим эту точку \(\displaystyle D{\small .}\)
Две точки, не принадлежащие прямой, расположены по разные её стороны тогда и только тогда, когда соединяющий их отрезок пересекает прямую.
В нашем рассуждении это точки \(\displaystyle B\) и \(\displaystyle C{\small .}\)
Они расположены по разные стороны прямой \(\displaystyle AK{\small .}\) Следовательно отрезок \(\displaystyle BC\) пересекает эту прямую.
Остаются два фрагмента. Один из них заканчивается требуемым выводом о том, что угол \(\displaystyle ABC\) острый.
На роль предпоследнего претендует только фрагмент, использующий свойство двух прямых, перпендикулярных данной.
4. Точки \(\displaystyle A\) и \(\displaystyle D\) расположены по одну сторону прямой \(\displaystyle BL{\small .}\) Иначе на прямой \(\displaystyle AK\) нашлась бы точка, принадлежащая прямой \(\displaystyle BL{\small .}\) Но это невозможно, так как прямые \(\displaystyle AK\) и \(\displaystyle BL\) перпендикулярны одной и той же прямой \(\displaystyle AB{\small .}\)
Две прямые, перпендикулярные третьей, не имеют общих точек.
В нашем рассуждении это прямые \(\displaystyle AK\) и \(\displaystyle BL{\small ,}\) перпендикулярные прямой \(\displaystyle AB{\small .}\)
У них нет общих точек, следовательно, отрезок \(\displaystyle AD\) не может пересекать прямую \(\displaystyle BL{\small .}\) Иными словами, точки \(\displaystyle A\) и \(\displaystyle D\) расположены по одну сторону прямой \(\displaystyle BL{\small .}\)
Остаётся последний фрагмент, утверждающий, что угол \(\displaystyle ABC\) острый по определению.
5. Значит, луч \(\displaystyle BD\) проходит во внутренней области угла \(\displaystyle ABL{\small .}\) Поэтому угол \(\displaystyle ABC\) является частью прямого угла \(\displaystyle ABL{\small ,}\) то есть острым углом.
Угол называется острым, если является частью прямого угла.
В настоящем рассуждении оказывается, что сторона угла \(\displaystyle ABC~-\) луч \(\displaystyle BD~-\) проходит во внутренней области прямого угла \(\displaystyle ABL{\small .}\)
Так что угол \(\displaystyle ABC~-\) часть угла \(\displaystyle ABL{\small .}\)