В одну сторону от луча \(\displaystyle AB\) отложены углы \(\displaystyle BAC\) и \(\displaystyle BAD\) величинами \(\displaystyle 73\degree \) и \(\displaystyle 136\degree \) соответственно.
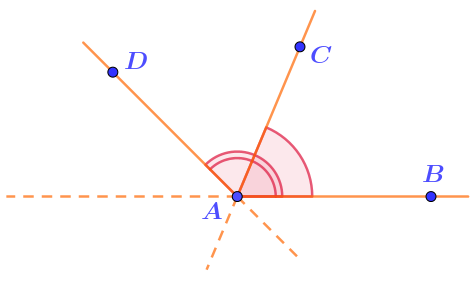
Найдите угол между прямыми \(\displaystyle AC\) и \(\displaystyle AD{\small .}\)
\(\displaystyle \degree \)
Угол \(\displaystyle DAC~-\) один из углов, образованных при пересечении прямых \(\displaystyle AC\) и \(\displaystyle AD{\small .}\)
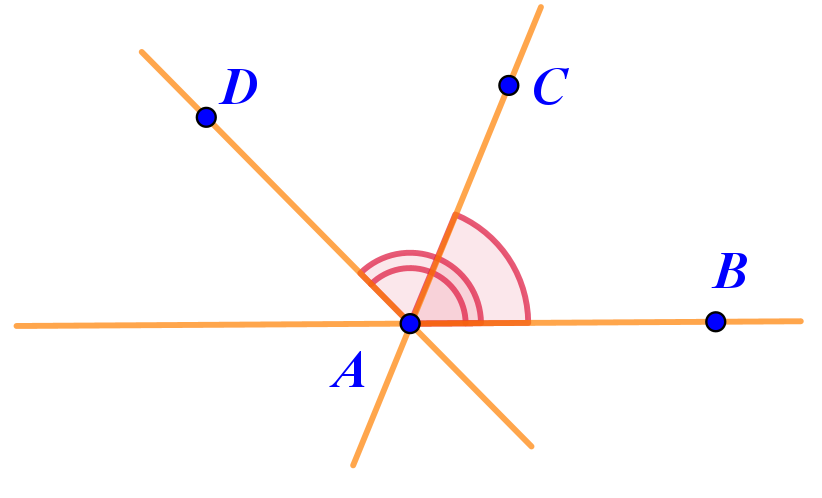
Он является частью угла \(\displaystyle BAD{\small .}\) Значит, его величина \(\displaystyle -\) разность величин углов \(\displaystyle BAD\) и \(\displaystyle BAC{\text :}\)
\(\displaystyle \angle DAC=136\degree-73\degree=63\degree{\small .}\)
Поскольку эта величина меньше \(\displaystyle 90\degree{\small ,}\) это и есть угол между прямыми.
Ответ: \(\displaystyle 63\degree{\small .}\)
