Даны несколько показаний часового табло в разное время.
Расставьте их в порядке возрастания величины угла между направлениями двух стрелок часов с циферблатом.
Для каждого из данных значений времени вычислим угол между направлениями стрелок.
Составим таблицу с показаниями табло и соответствующими им углами между направлениями стрелок.
В каждом случае сделаем рисунок и поделим соответствующий угол с вершиной в центре циферблата на две части.
Для этого проведём луч с началом в центре циферблата, проходящий во внутренней области угла, так, чтобы:
- он проходил через метку часовой разметки;
- величина \(\displaystyle \beta\) образовавшейся части, ограниченной направлением часовой стрелки, была наименьшей.
| Табло | Рисунок | Вычисление угла |
| \(\displaystyle 02:32\) | 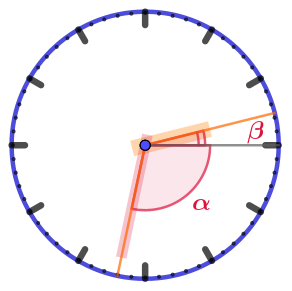 | Угол величиной \(\displaystyle \alpha\) заключает ровно \(\displaystyle 17\) делений минутной разметки. Значит, \(\displaystyle \alpha=17\cdot 6\degree =102\degree{\small .} \) До конца часа, когда часовая стрелка достигнет метки часовой разметки, она будет двигаться \(\displaystyle 28\) минут. Значит \(\displaystyle \beta=28\cdot 0{,}5\degree =14\degree {\small .}\) Искомый угол: \(\displaystyle \alpha+\beta=102\degree +14\degree =116\degree{\small .} \) |
| \(\displaystyle 03:41\) | 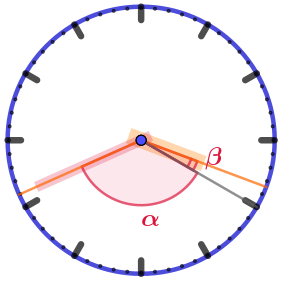 | Угол величиной \(\displaystyle \alpha\) заключает ровно \(\displaystyle 21\) деление минутной разметки. Значит, \(\displaystyle \alpha=21\cdot 6\degree =126\degree{\small .} \) До конца часа, когда часовая стрелка достигнет метки часовой разметки, она будет двигаться \(\displaystyle 19\) минут. Значит \(\displaystyle \beta=19\cdot 0{,}5\degree =9{,}5\degree {\small .}\) Искомый угол: \(\displaystyle \alpha+\beta=126\degree +9{,}5\degree =135{,}5\degree{\small .} \) |
| \(\displaystyle 14:35\) | 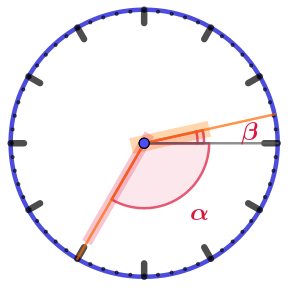 | Угол величиной \(\displaystyle \alpha\) заключает ровно \(\displaystyle 20\) делений минутной разметки. Значит, \(\displaystyle \alpha=20\cdot 6\degree =120\degree{\small .} \) До конца часа, когда часовая стрелка достигнет метки часовой разметки, она будет двигаться \(\displaystyle 25\) минут. Значит \(\displaystyle \beta=25\cdot 0{,}5\degree =12{,}5\degree {\small .}\) Искомый угол: \(\displaystyle \alpha+\beta=120\degree +12{,}5\degree =132{,}5\degree{\small .} \) |
| \(\displaystyle 18:15\) | 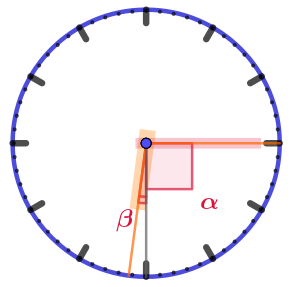 | Угол величиной \(\displaystyle \alpha\) заключает ровно \(\displaystyle 15\) делений минутной разметки. Значит, \(\displaystyle \alpha=15\cdot 6\degree =90\degree{\small .} \) С начала часа, когда часовая стрелка указывала на метку часовой разметки, она двигалась \(\displaystyle 15\) минут. Значит \(\displaystyle \beta=15\cdot 0{,}5\degree =7{,}5\degree {\small .}\) Искомый угол: \(\displaystyle \alpha+\beta=90\degree +7{,}5\degree =97{,}5\degree{\small .} \) |
| \(\displaystyle 97{,}5\degree\) | \(\displaystyle <\) | \(\displaystyle 116\degree\) | \(\displaystyle <\) | \(\displaystyle 132{,}5\degree\) | \(\displaystyle <\) | \(\displaystyle 135{,}5\degree\) |
| \(\displaystyle 18:15\) | \(\displaystyle 02:32\) | \(\displaystyle 14:35\) | \(\displaystyle 03:41\) |
| Ответ: |  |