Найдите величины углов, которые стрелки часов образуют со своими первоначальными положениями через \(\displaystyle 100\) минут после начала наблюдений.
Угол между начальным и конечным направлениями часовой стрелки: \(\displaystyle \alpha =\)\(\displaystyle \degree \)
Угол между начальным и конечным направлениями минутной стрелки: \(\displaystyle \beta =\)\(\displaystyle \degree \)
Стрелки движутся по циферблату часов равномерно. То есть за равные промежутки времени меняют своё положение на один и тот же угол.
- Часовая стрелка меняет своё положение на развёрнутый угол за \(\displaystyle 6\) часов. То есть за минуту она меняет своё положение на половину градуса. Часовое деление она проходит за час. Значит, минутное деление она преодолевает за \(\displaystyle 12\) минут.
- Минутная стрелка меняет своё положение на развёрнутый угол за половину часа. То есть за минуту она меняет своё положение на \(\displaystyle 6\degree{\small .}\) Очевидно, минутное деление она проходит за минуту, а часовое \(\displaystyle -\) за пять.
Стрелки движутся по циферблату в одну сторону (говорят: "по часовой стрелке").
Значит, угол между направлениями стрелок меняется равномерно с угловой скоростью, равной разности скоростей стрелок.
А именно, увеличивается или уменьшается на \(\displaystyle 6\degree -30'=5\degree 30'\) в минуту.
Для определённости предположим, что наблюдения начались в полдень.
В этот момент направления стрелок совпадали: обе были направлены вертикально вверх.
Спустя \(\displaystyle 100\) минут часы будут показывать без двадцати два. На рисунке изобразим часы в этот момент и отметим нужные углы.
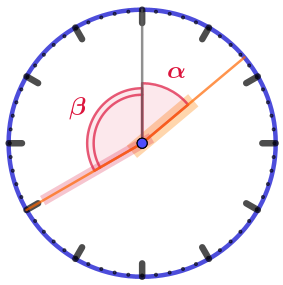
Часовая стрелка проходила половину градуса каждую минуту. Таким образом,
\(\displaystyle \alpha=100\cdot 0{,}5\degree =\textcolor{green}{50\degree {\small .}}\)
Минутной стрелке остаётся четыре полных деления часовой разметки. Каждое деление составляет шестую часть развёрнутого угла, то есть \(\displaystyle 30\degree {\small .}\) Значит,
\(\displaystyle \beta=4\cdot 30\degree = \textcolor{green}{120\degree {\small .}}\)
Можно применить к вычислению второго угла тот же способ, что и при вычислении первого.
Важно сделать это правильно. Простое умножение минут на градусы даст слишком большое значение, не соответствующее величине никакого угла.
Для корректного применения способа заметим, что в первоначальное положение минутная стрелка вернётся через \(\displaystyle 20\) минут.
За одну минуту минутная стрелка проходит \(\displaystyle 6\degree {\small .}\) Значит,
\(\displaystyle \beta=20\cdot 6\degree = 120\degree {\small .}\)
Ответ: \(\displaystyle \alpha=50\degree{\small ,\;}\beta=120\degree {\small .}\)