Сопоставьте каждому показанию часов с циферблатом угол между направлениями их стрелок.
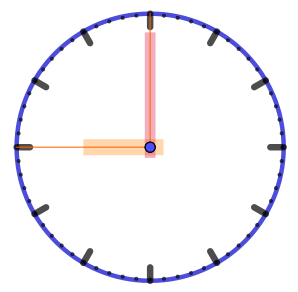 | 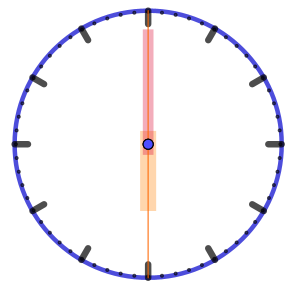 | 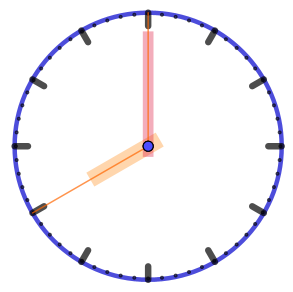 | 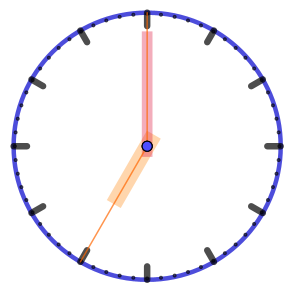 | 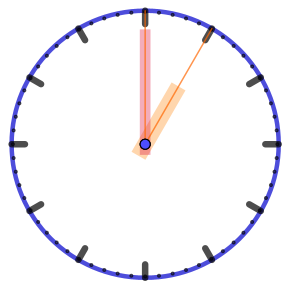 |
Циферблат часов разделён на \(\displaystyle 12\) равных частей (часовая разметка).
Каждая из этих частей, разделена ещё на \(\displaystyle 5\) равных частей (минутная разметка).
Рассмотрим развёрнутый угол с вершиной в центре циферблата. Он составлен из шести равных частей.
Угол, стороны которого \(\displaystyle -\) лучи с началом в центре циферблата, проходящие через соседние метки часовой разметки, имеет величину \(\displaystyle \frac{180\degree }{6}=30\degree {\small .}\) | 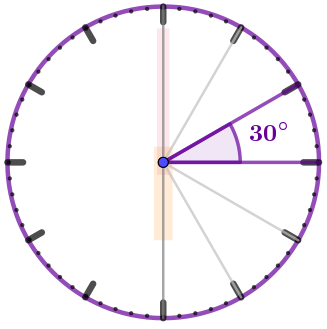 |
Угол, стороны которого \(\displaystyle -\) лучи с началом в центре циферблата, проходящие через соседние метки минутной разметки, имеет величину \(\displaystyle \frac{30\degree }{5}=6\degree {\small .}\) | 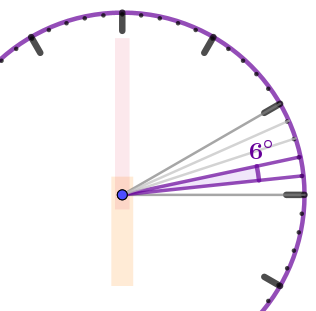 |
| Угол, образованный стрелками | Величина угла |
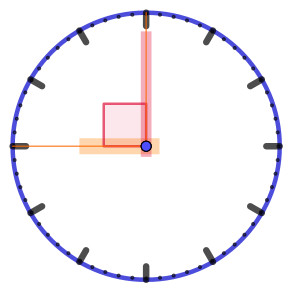 | Угол охватывает ровно три часовых деления. Его величина \(\displaystyle 3\cdot 30\degree =90\degree {\small .}\) |
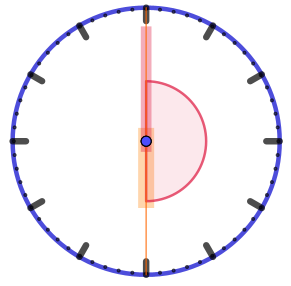 | Угол охватывает ровно шесть часовых делений. Его величина \(\displaystyle 6\cdot 30\degree =180\degree {\small .}\) |
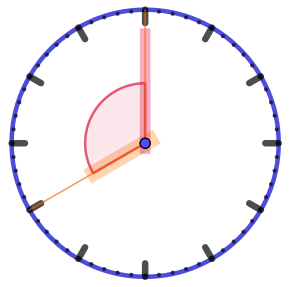 | Угол охватывает ровно четыре часовых деления. Его величина \(\displaystyle 4\cdot 30\degree =120\degree {\small .}\) |
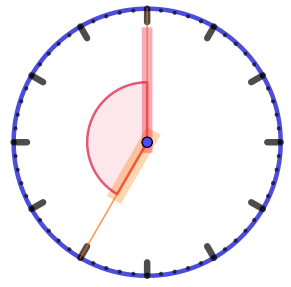 | Угол охватывает ровно пять часовых делений. Его величина \(\displaystyle 5\cdot 30\degree =150\degree {\small .}\) |
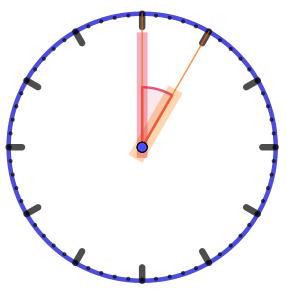 | Угол охватывает ровно одно часовое деление. Его величина \(\displaystyle 30\degree {\small .}\) |
| Ответ: | 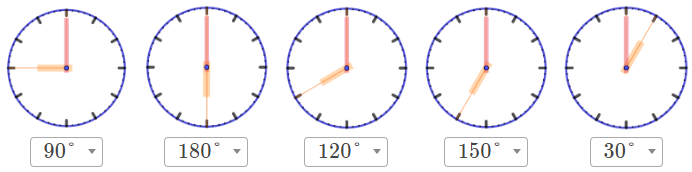 |