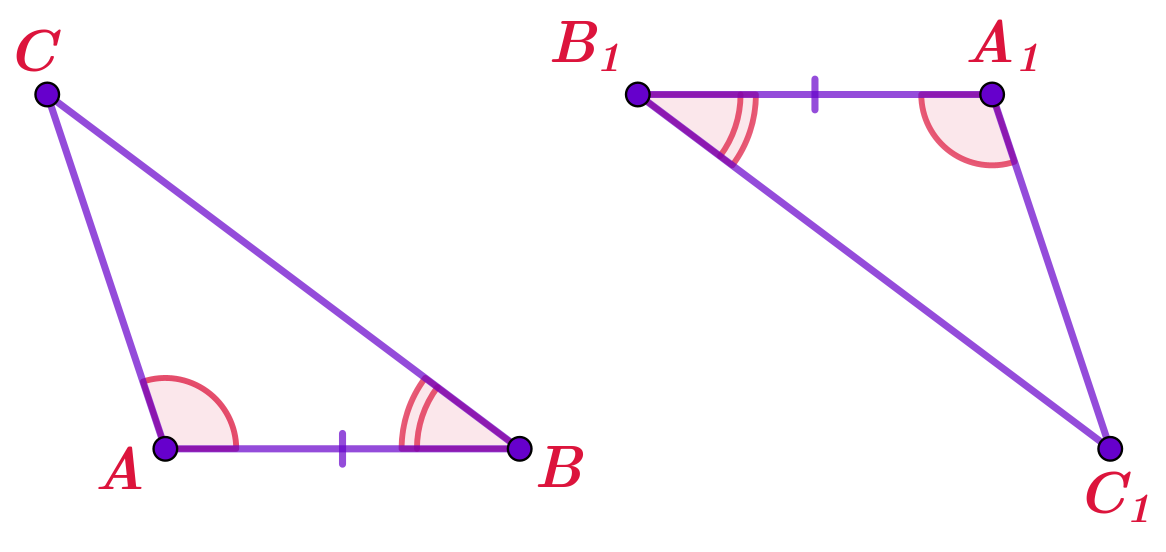
На рисунке треугольник \(\displaystyle ABC\) и ещё три треугольника. Отмечены равные элементы.
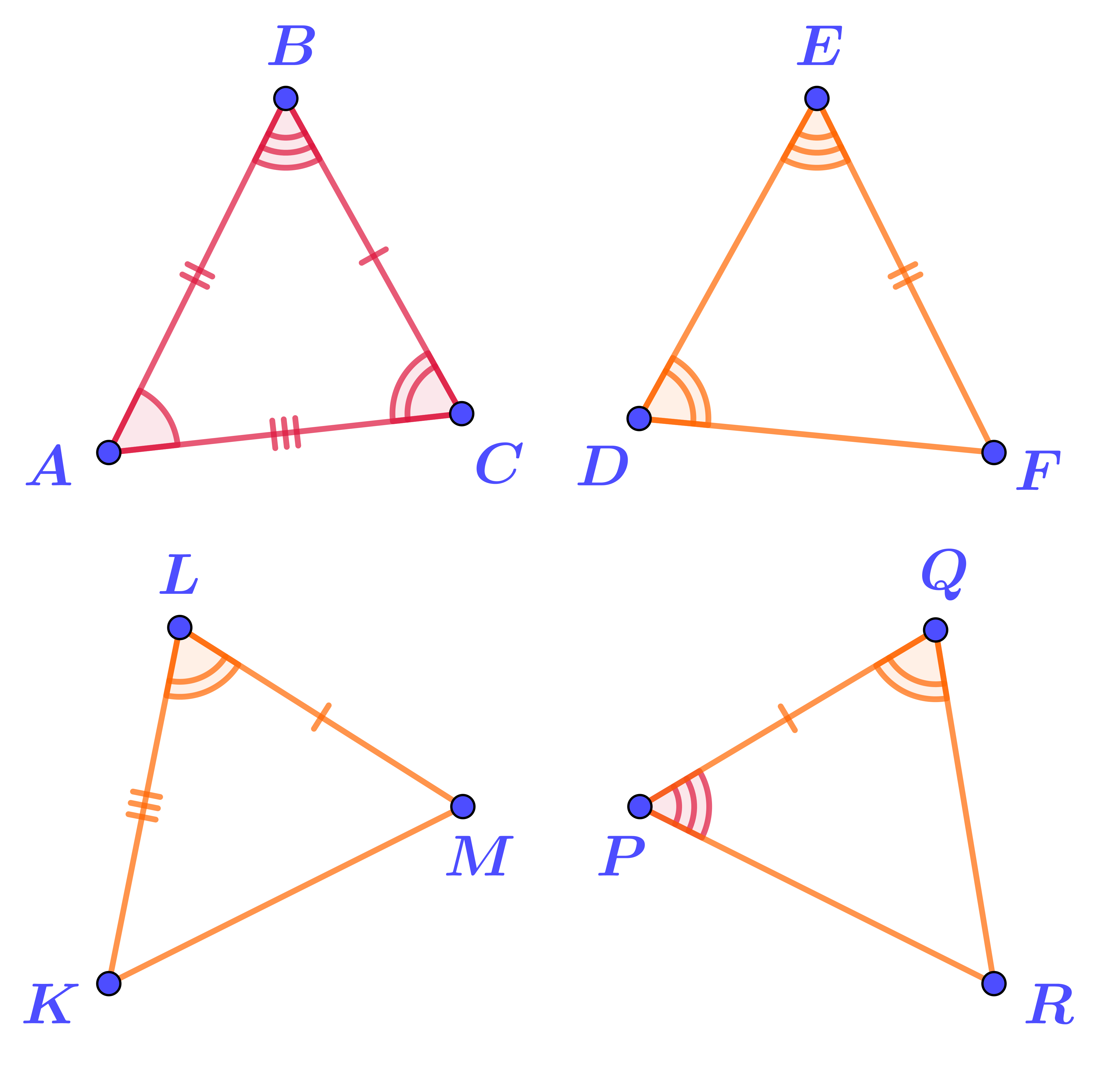
Выберите треугольник, равный треугольнику \(\displaystyle ABC\) по второму признаку равенства.
Для каждой пары треугольников, один из которых треугольник \(\displaystyle ABC{\small ,}\) проверим, можно ли применить второй признак равенства треугольников.
В треугольнике \(\displaystyle DEF\) есть два отмеченных угла, равных углам треугольника \(\displaystyle ABC{\small .}\)
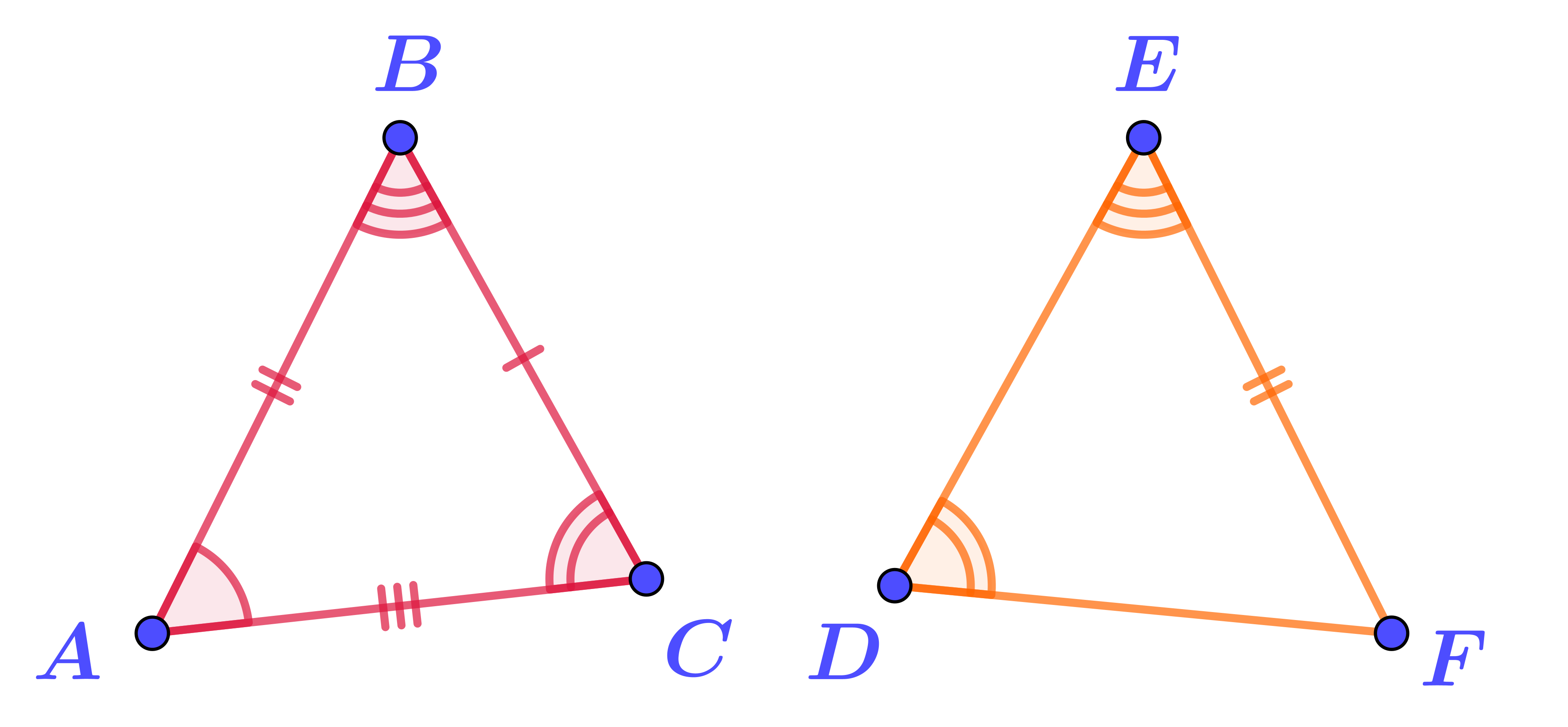
Однако сторона \(\displaystyle DE{ \small ,}\) к которой эти углы прилежат, не отмечена как равная стороне \(\displaystyle BC\) треугольника \(\displaystyle ABC{\small .}\)
Значит, применить второй признак равенства треугольников нельзя.
Для применения второго признака равенства треугольников необходимы две пары равных углов.
Но в треугольнике \(\displaystyle KLM\) отмечен только один угол, равный углу треугольника \(\displaystyle ABC{\small .}\)
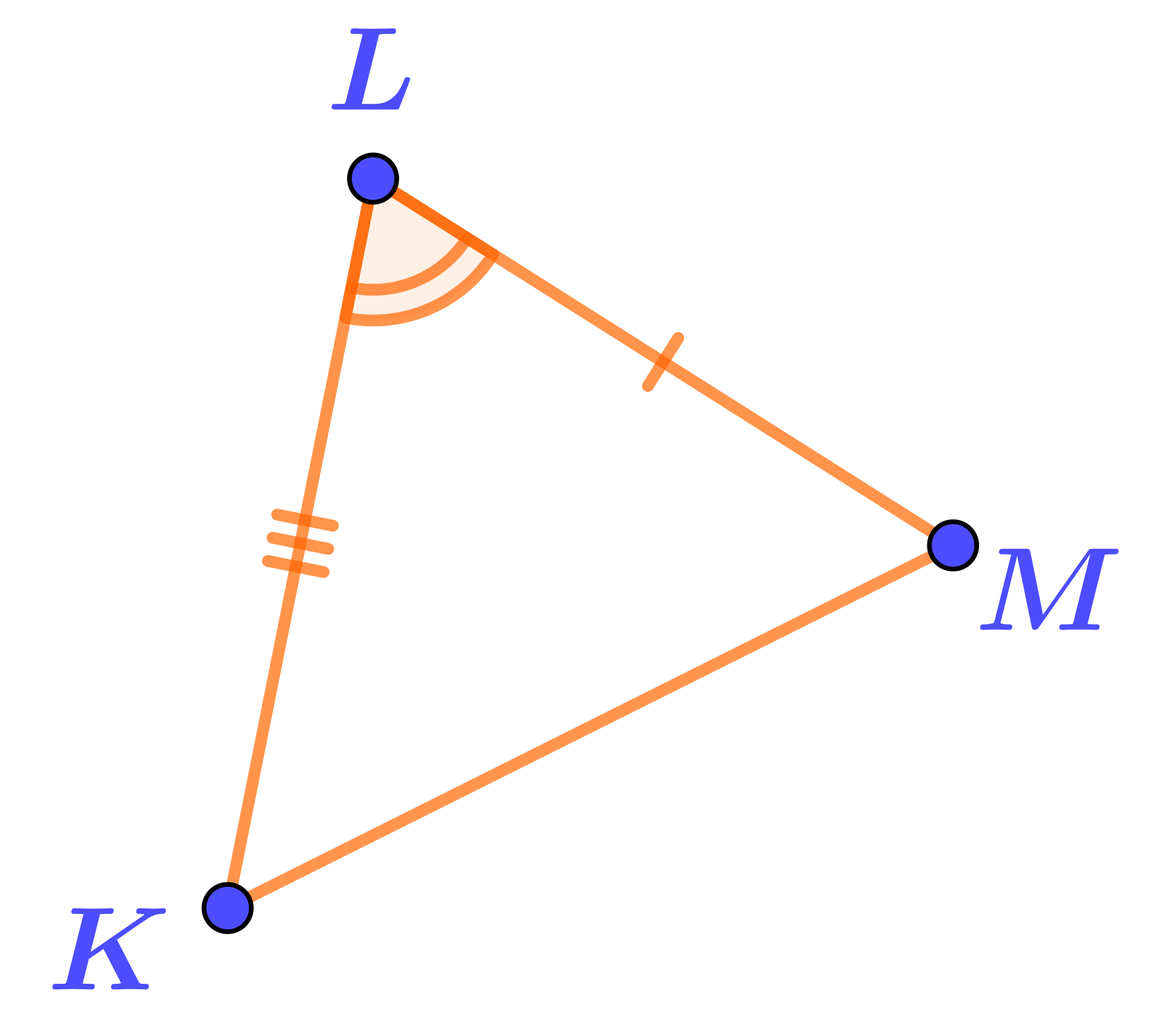
Значит, применить второй признак равенства треугольников нельзя.
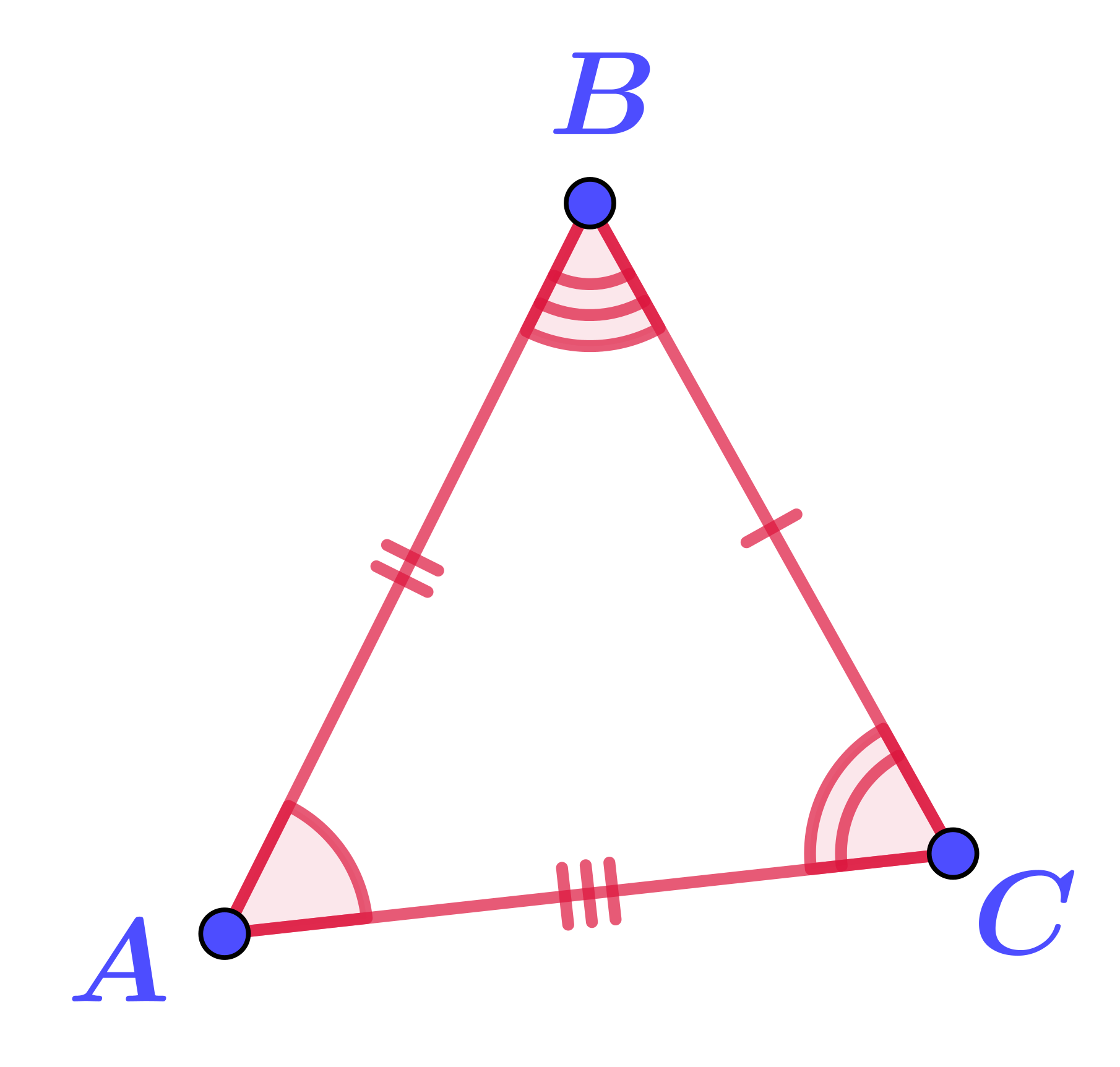
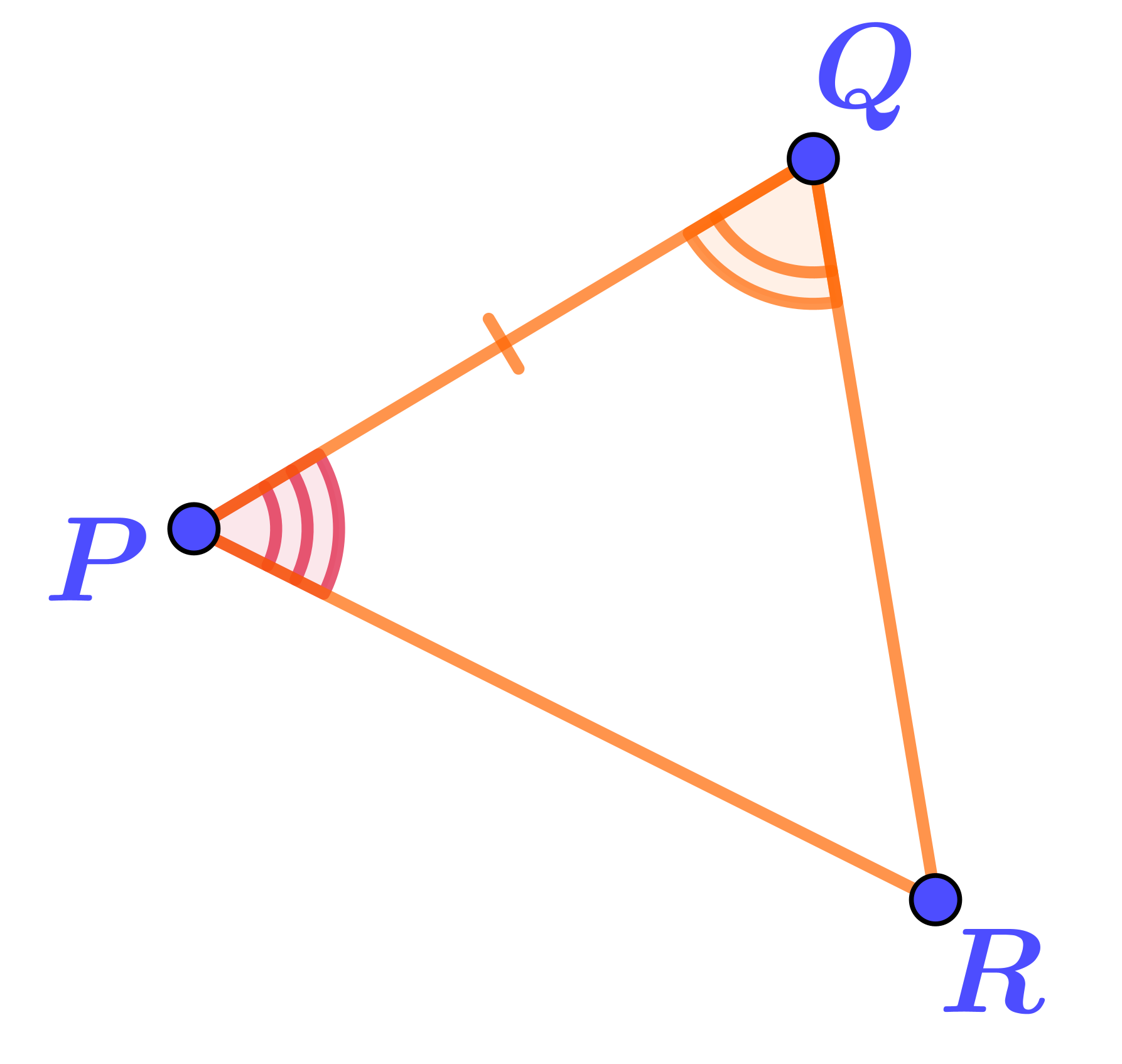
В этих треугольниках
\(\displaystyle \left\{\begin{array}{ll}BC=PQ\\\angle ABC=\angle QPR\\\angle BCA=\angle RQP\end{array}{\LARGE\Rightarrow} \quad {\bf\triangle}ABC={\bf\triangle}RPQ\text{ \normalsize\it(по второму признаку)}\right.\)
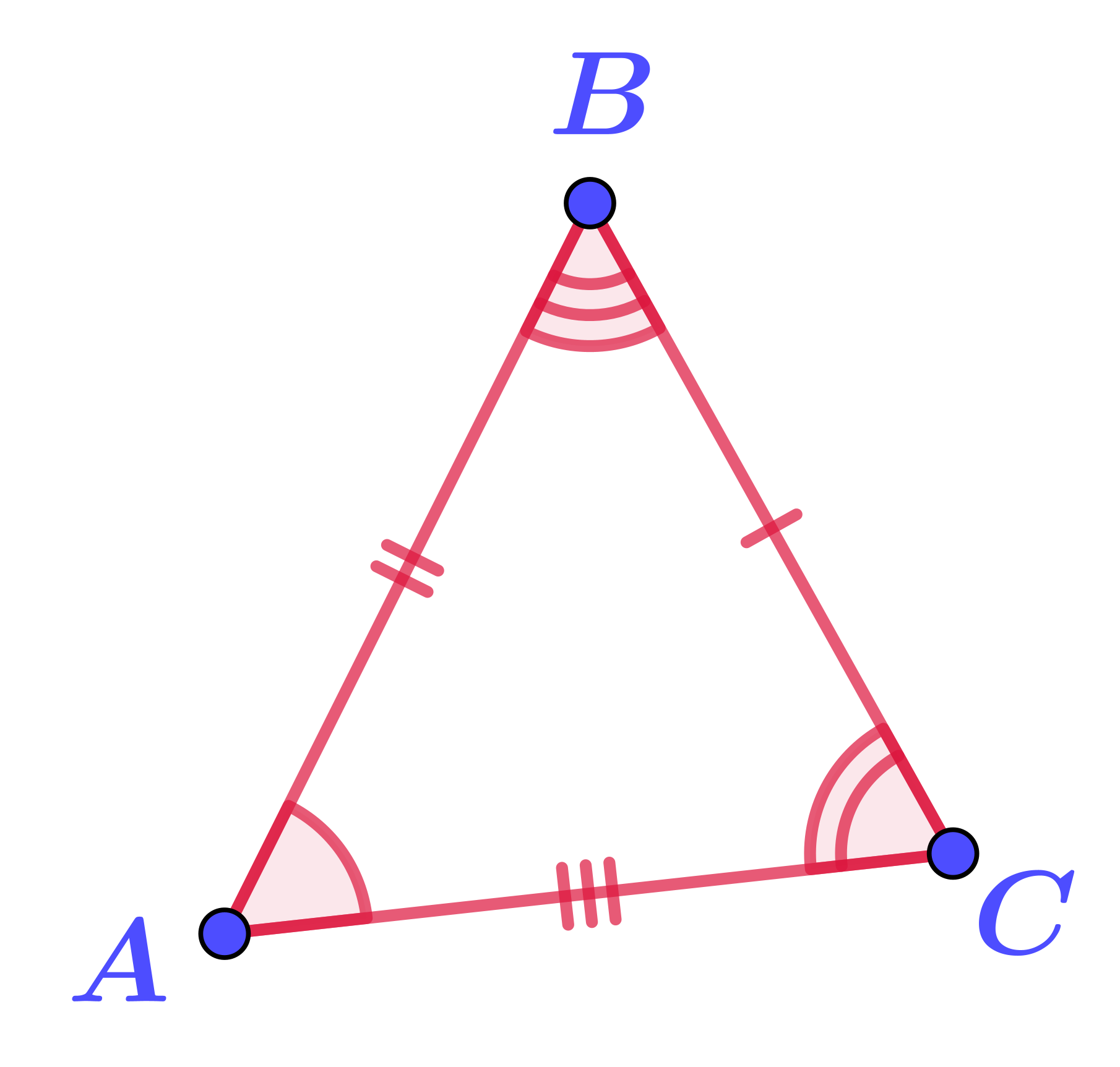
Треугольники \(\displaystyle ABC\) и \(\displaystyle RPQ\) равны по стороне и двум прилежащим к ней углам.
Ответ: \(\displaystyle {\triangle}RPQ {\small .}\)