Какая из следующих записей доказывает равенство треугольников по второму признаку равенства?
Заметим, что во всех вариантах ответа среди исходных равенств есть \(\displaystyle AC=PQ{\small .}\)
Изобразим два равных треугольника \(\displaystyle ABC\) и \(\displaystyle PSQ\) с равными сторонами \(\displaystyle AC\) и \(\displaystyle PQ{\small .}\)
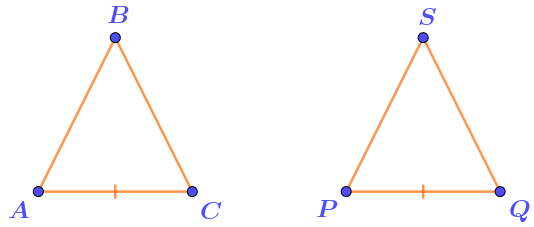
Выпишем в этих треугольниках обозначения углов, прилежащих к равным сторонам \(\displaystyle AC\) и \(\displaystyle PQ{\text :}\)
- в треугольнике \(\displaystyle ABC\) это углы \(\displaystyle BAC\) и \(\displaystyle BCA{\small ,}\)
- в треугольнике \(\displaystyle PSQ\) это углы \(\displaystyle SPQ\) и \(\displaystyle SQP{\small .}\)
Из двух способов составления пар равных углов из выписанных обозначений один находим в предложенных вариантах ответа.
Ответ: \(\displaystyle \left\{ \begin{array}{ll} AC=PQ\\ \angle BAC=\angle SPQ\\ \angle BCA=\angle SQP \end{array} {\LARGE\Rightarrow} \quad {\bf\triangle}\!ABC={\bf\triangle}\!PSQ\text{ \normalsize\it(по второму признаку)} \right. \)