На плоскости отмечены точки \(\displaystyle A{\small ,\;}B{\small ,\;}C{\small ,\;}D{\small ,\;}E\) и \(\displaystyle F{\small .}\)
Известно, что \(\displaystyle BC=EF{\small ,\;}\)\(\displaystyle \angle DBC=\angle AEF{\small ,\;}\)\(\displaystyle \angle DCB=\angle AFE{\small .}\)
Какой вывод можно сделать, пользуясь вторым признаком равенства треугольников?
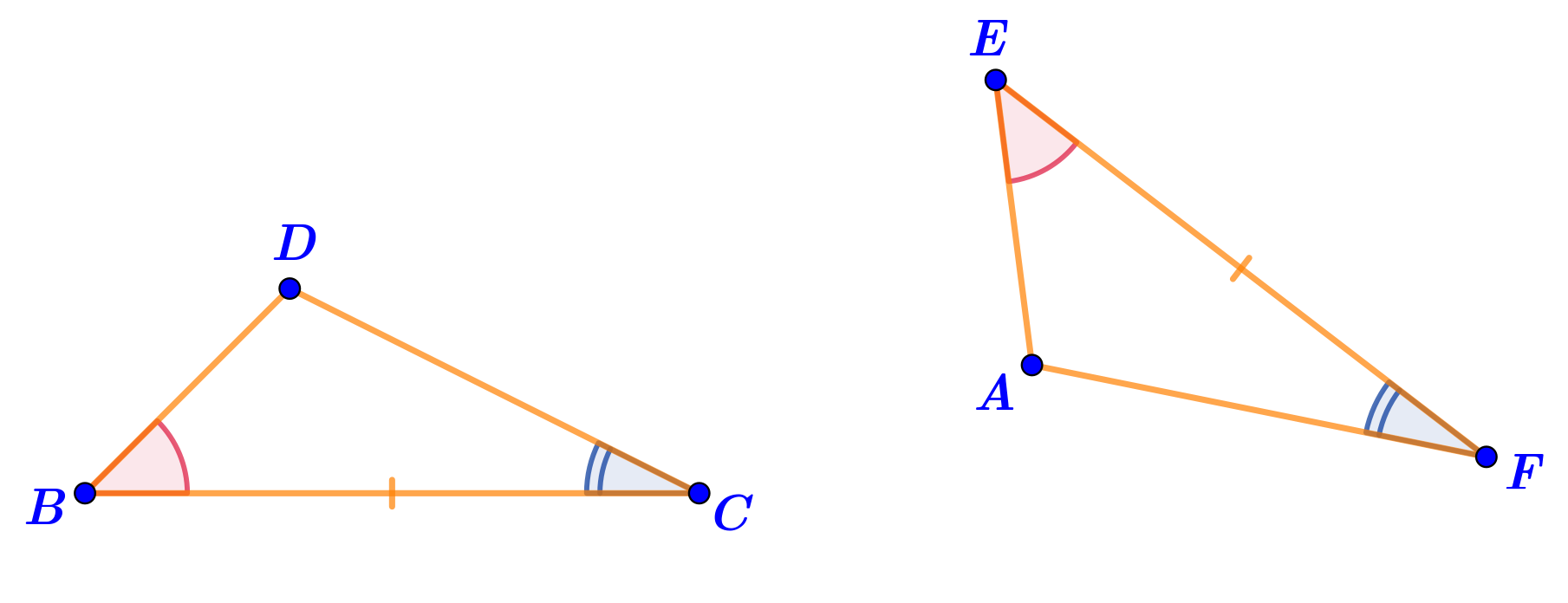
Изобразим отрезки и углы, удовлетворяющие условию задачи. Начинать лучше всего с равных отрезков \(\displaystyle BC\) и \(\displaystyle EF{\small .}\)
Далее нужно отложить равные (лучше всего острые) углы от лучей \(\displaystyle BC\) и \(\displaystyle EF{\small .}\) Затем \(\displaystyle -\) от лучей \(\displaystyle CB\) и \(\displaystyle FE{\small .}\)
Точки пересечения проведённых сторон углов подписывавем \(\displaystyle D\) и \(\displaystyle A{\small .}\) Отмечаем все равные элементы.
\(\displaystyle \begin{cases}\\\\\\\\\\\\\end{cases} \) | \(\displaystyle BC=FE\) | \(\displaystyle {\LARGE\Rightarrow}\) |
|
| \(\displaystyle {\bf\angle}DBC = {\bf\angle}AEF\) | \(\displaystyle {\triangle}DBC={\triangle}AEF\) | ||
| \(\displaystyle {\bf\angle}DCB = {\bf\angle}AFE\) | (по второму признаку) |
Ответ: \(\displaystyle {\triangle}DBC={\triangle}AEF{\small .}\)