Задание
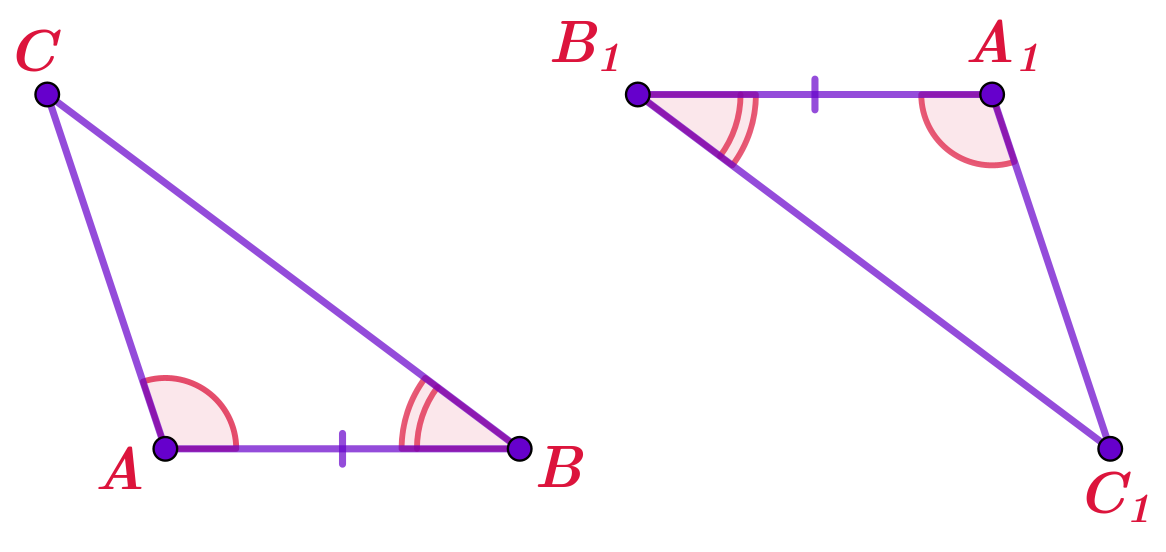
На рисунке треугольники, равенство которых доказывается по второму признаку.
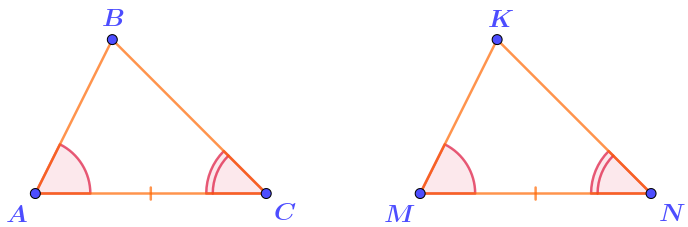
Заполните пропуски в доказательстве.
\(\displaystyle \begin{cases}\\\\\\\\\\\\\end{cases} \) | \(\displaystyle AC= MN\) | \(\displaystyle {\LARGE\Rightarrow}\) |
|
| \(\displaystyle {\bf\angle}BCA = {\bf\angle}KNM\) | (по второму признаку) |
Решение
Треугольники \(\displaystyle ABC\) и \(\displaystyle MKN\) равны по стороне и двум прилежащим к ней углам
В левой части выражения, доказывающего равенство треугольников, должны быть указаны две пары равных углов и пара равных сторон.
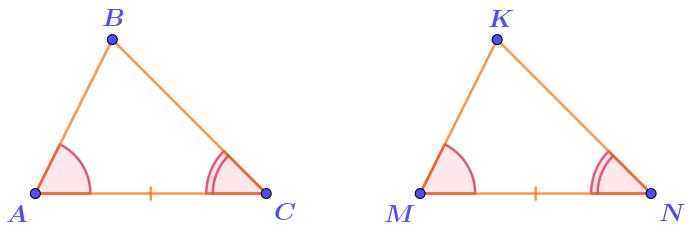
Находим по рисунку недостающую пару равных углов и вписываем в левую часть выражения.
В правую помещаем вывод о равенстве треугольников:
\(\displaystyle \begin{cases}\\\\\\\\\\\\\end{cases} \) | \(\displaystyle AC= MN\) | \(\displaystyle {\LARGE\Rightarrow}\) |
|
| \(\displaystyle \color{green}{{{\bf\angle}BAC = {\bf\angle}KMN}}\) | \(\displaystyle \color{green}{{{\bf\triangle}ABC={\bf\triangle}MKN}}\) | ||
| \(\displaystyle {\bf\angle}BCA = {\bf\angle}KNM\) | (по второму признаку) |
Ответ: пропущенные выражения –\(\displaystyle {\bf\angle}BAC = {\bf\angle}KMN{\small ,}\) \(\displaystyle {\bf\triangle}ABC={\bf\triangle}MKN{\small .}\)