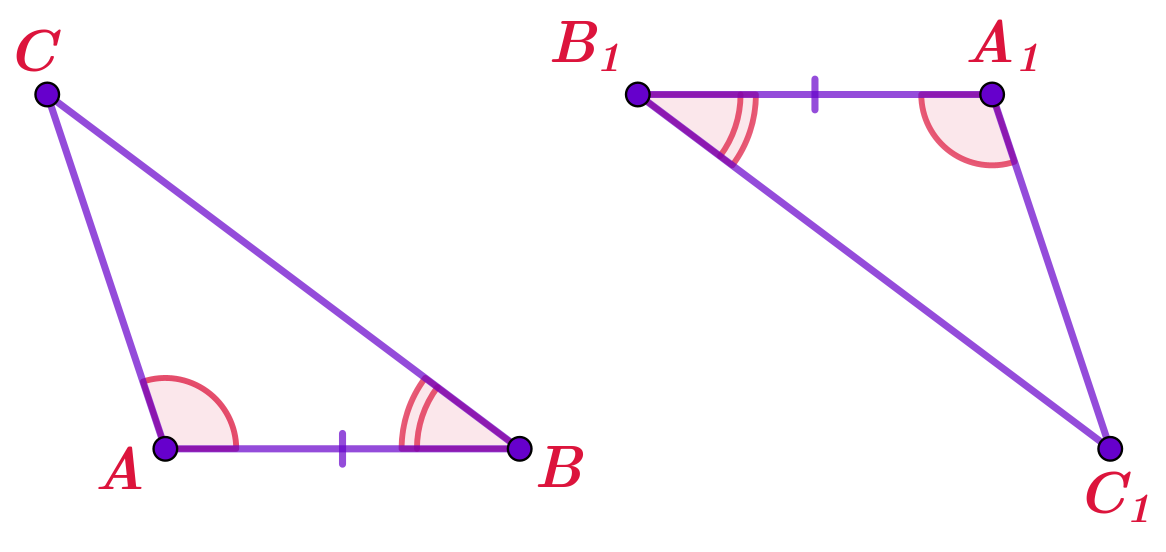
На сторонах треугольника \(\displaystyle ABC\) построены ещё три треугольника. На рисунке отмечены равные элементы.
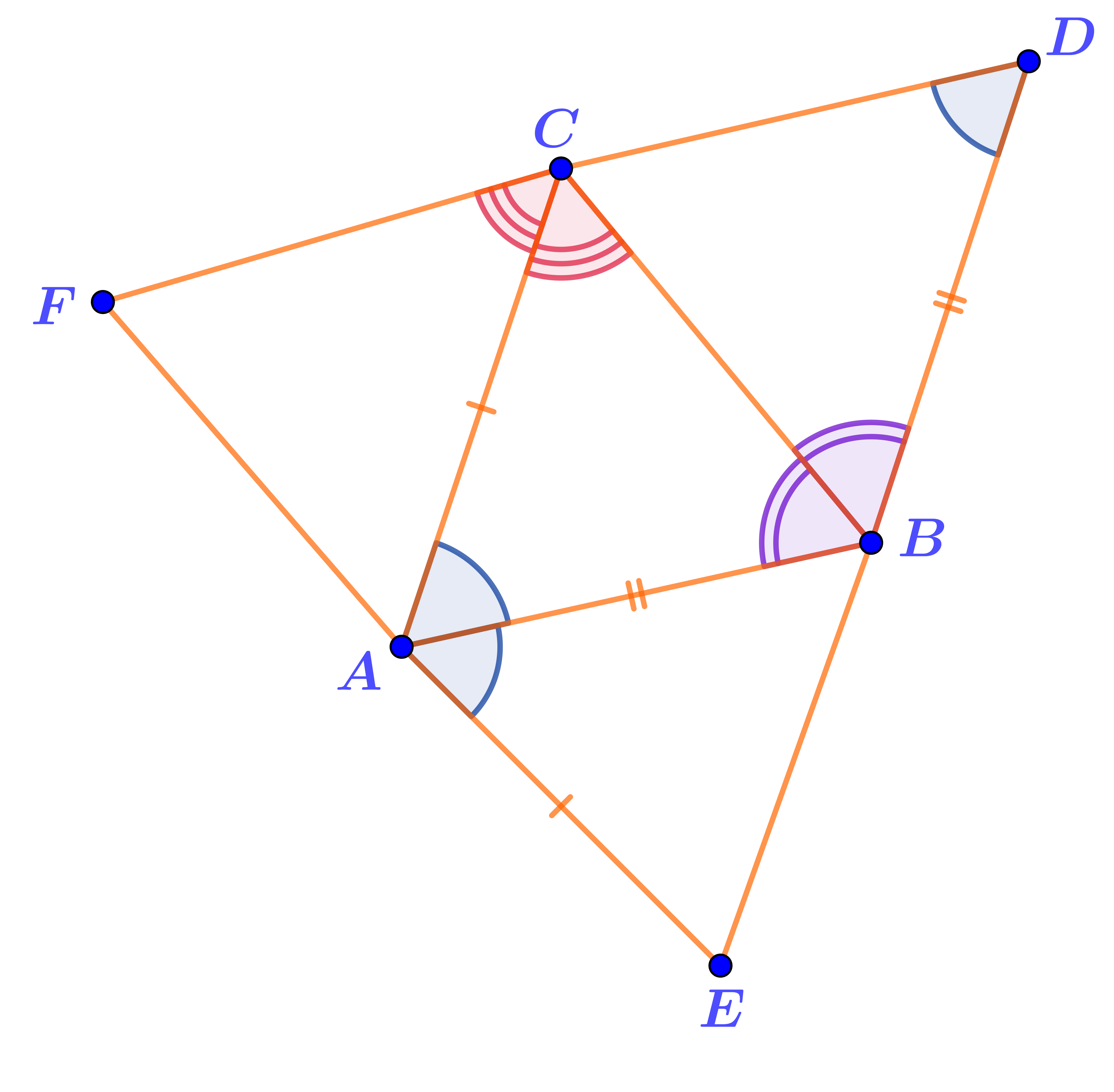
Равенство какого из них треугольнику \(\displaystyle ABC\) можно доказать, пользуясь вторым признаком равенства треугольников?
В этих треугольниках не обнаруживается двух пар равных углов.
Есть только общая сторона и одна пара равных углов.
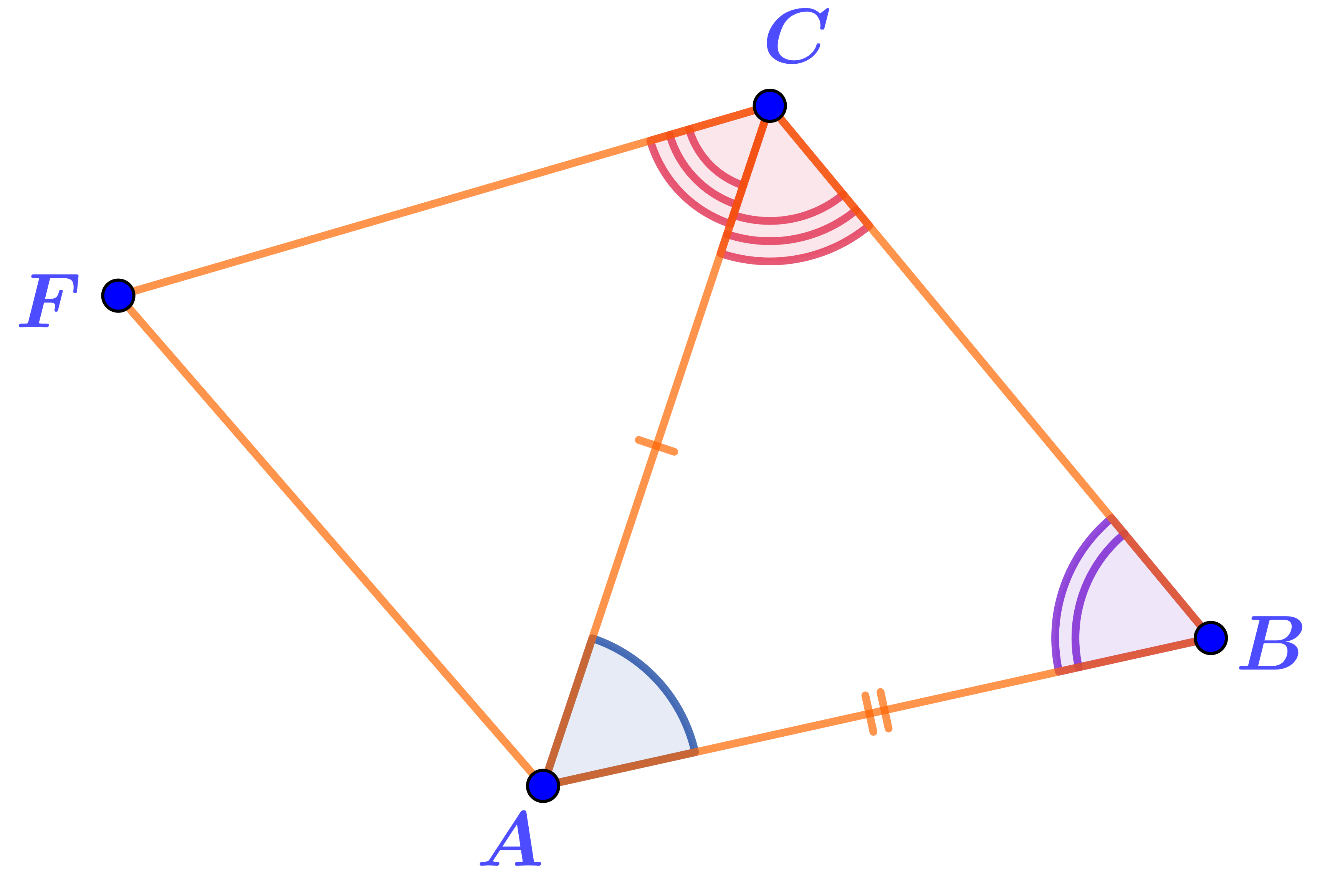
В этих треугольниках:
- \(\displaystyle AB=BD{\small ;}\)
- \(\displaystyle \angle CAB=\angle CDB{\small ;}\)
- \(\displaystyle \angle CBA=\angle DBC{\small .}\)
Заметим, что равны именно углы, прилежащие к равными сторонам \(\displaystyle AB\) и \(\displaystyle BD{\small .}\)
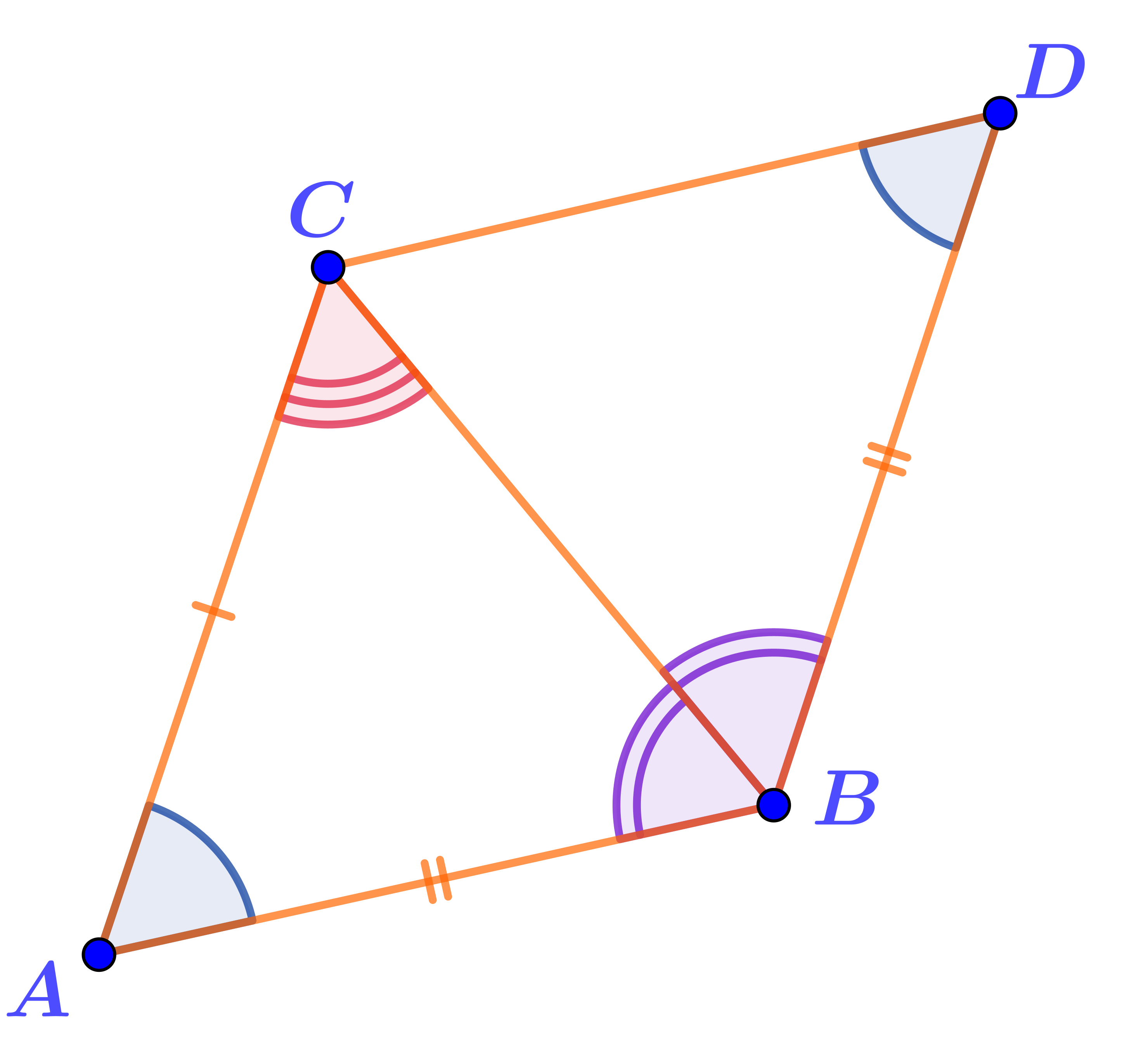
Условия второго признака выполняются.
Треугольники \(\displaystyle ABC\) и \(\displaystyle DBC\) равны по стороне и двум прилежащим к ней углам.
В этих треугольниках:
- \(\displaystyle AC=AE{\small ;}\)
- сторона \(\displaystyle AE\) общая;
- \(\displaystyle \angle CAB=\angle BAE{\small .}\)
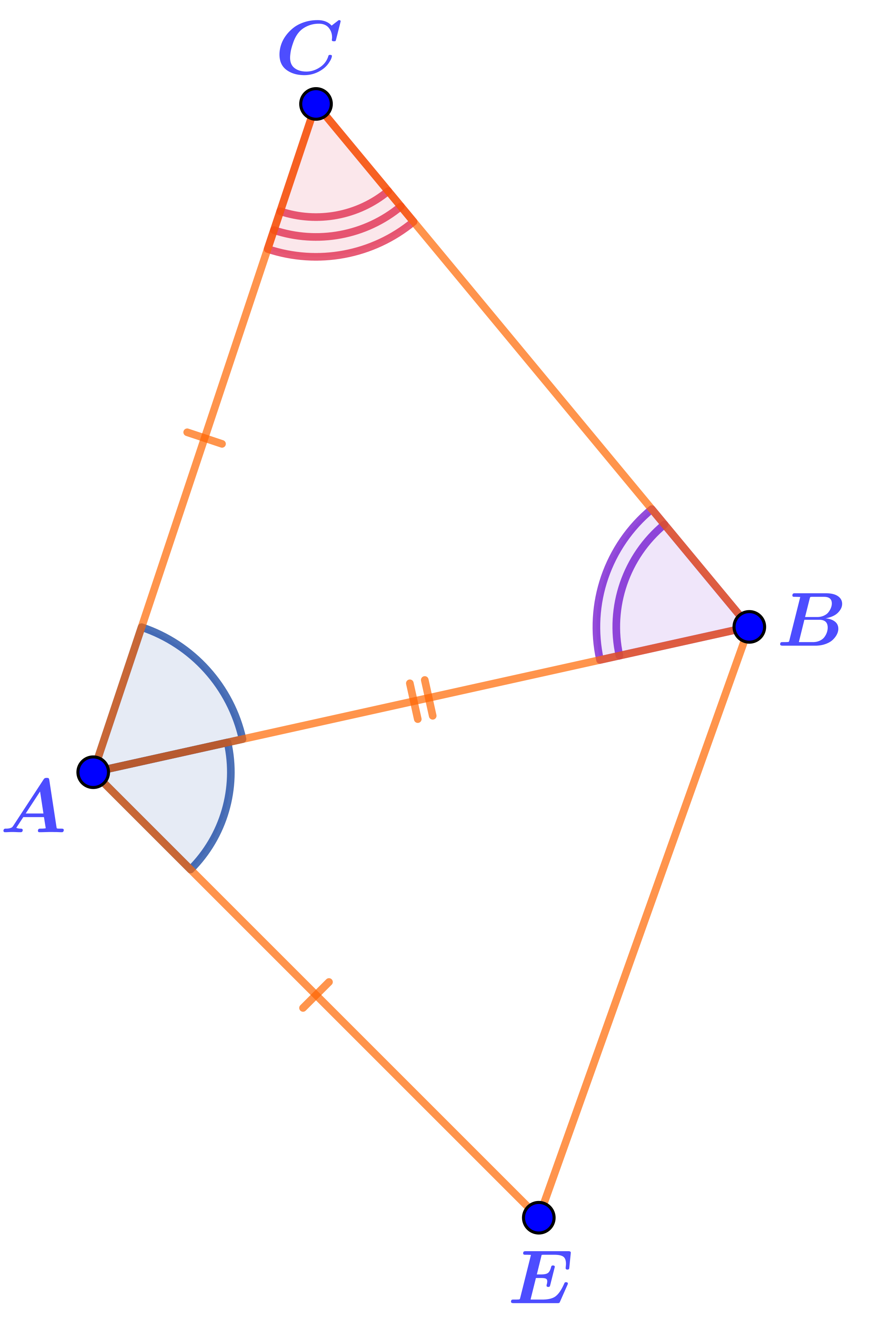
Треугольники равны по первому признаку. Это позволяет получить вторую пару равных углов, которой не хватает для применения второго признака равенства треугольников.
Но, поскольку равенство треугольников уже доказано, применение второго признака лишено всякого смысла.
Ответ: \(\displaystyle {\triangle}ABC={\triangle}DBC\) по второму признаку равенства треугольников.