На рисунке треугольники, равенство которых доказывается по второму признаку.
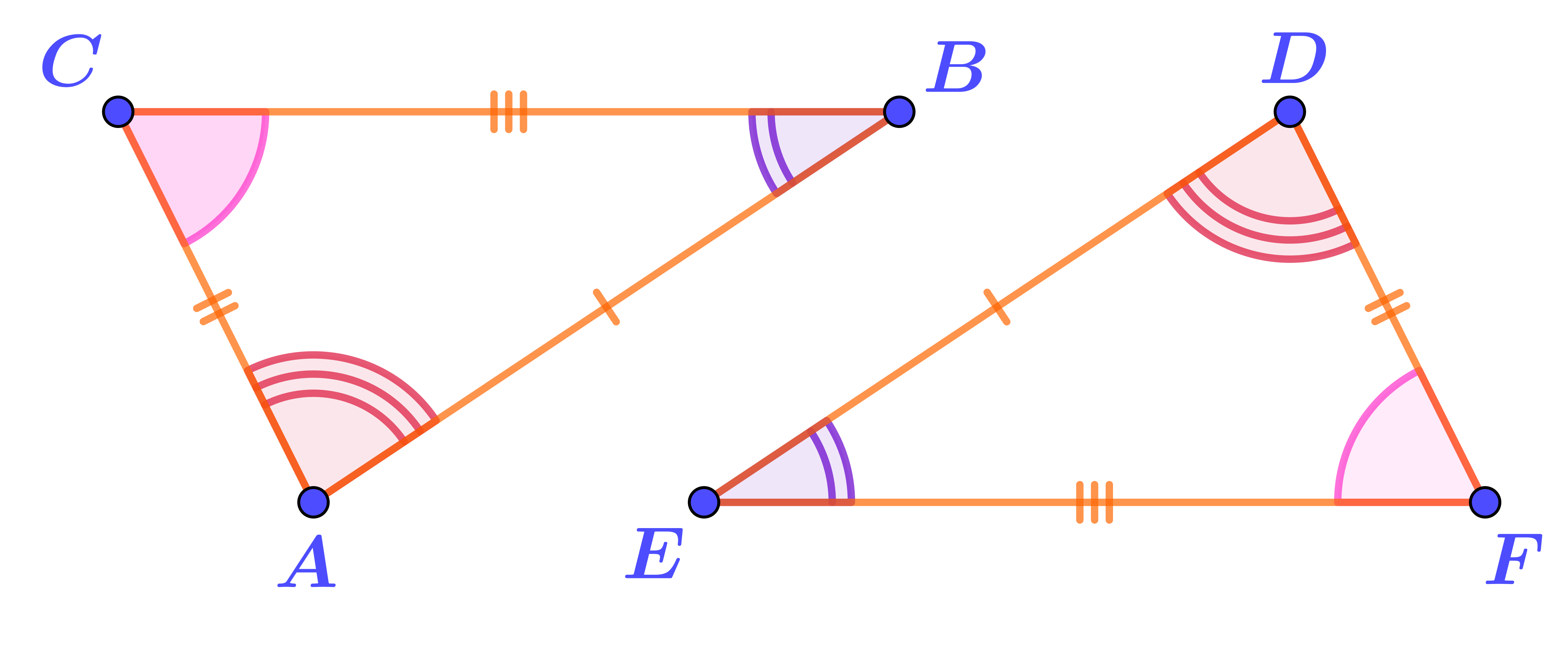
Выберите запись, соответствующую этому доказательству.
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то треугольники равны.
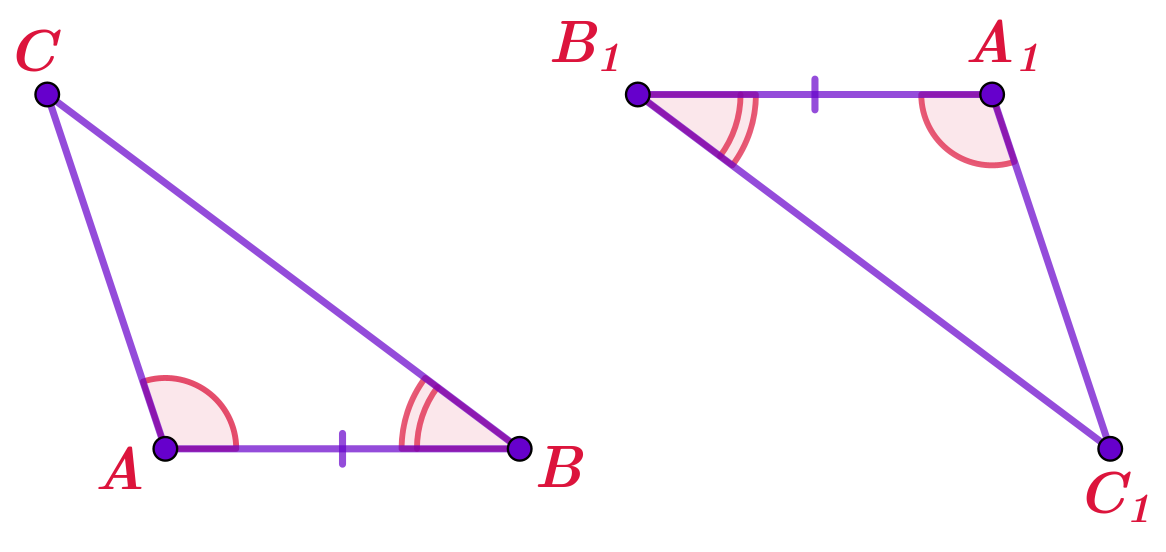
\(\displaystyle\left\{\begin{array}{}AB=A_1B_1\\\angle A=\angle A_1\\\angle B=\angle B_1\end{array} {\LARGE\Rightarrow} \quad {\bf\triangle}ABC={\bf\triangle}A_1B_1C_1\right.\)
Запись, соответствующая этому доказательству, содержит равенства пары сторон и двух пар углов треугольников:
\(\displaystyle \begin{cases}\\\\\\\\\\\\\end{cases} \) | \(\displaystyle BC= EF\) | \(\displaystyle {\LARGE\Rightarrow}\) |
|
| \(\displaystyle {\bf\angle}ACB = {\bf\angle}EFD\) | \(\displaystyle {\triangle}ABC={\triangle}DEF\) | ||
| \(\displaystyle {\bf\angle}CBA = {\bf\angle}DEF\) | (по второму признаку) |
Важно проверить, что равные углы прилежат именно к равным сторонам. В данном случае это именно так: Обозначения концов отрезков соответствуют обозначениям вершин углов:
| \(\displaystyle {\bf\angle}C{\textcolor{orange}B}A = {\bf\angle}D{\textcolor{orange}E}F{\small ,\;}\) | \(\displaystyle \textcolor{orange}{B}\textcolor{magenta}{C}= {\textcolor{orange}E}\textcolor{magenta}{F}{\small ,\;}\) | \(\displaystyle {\bf\angle}A\textcolor{magenta}{C}B = {\bf\angle}E\textcolor{magenta}{F}D{\small .}\) |