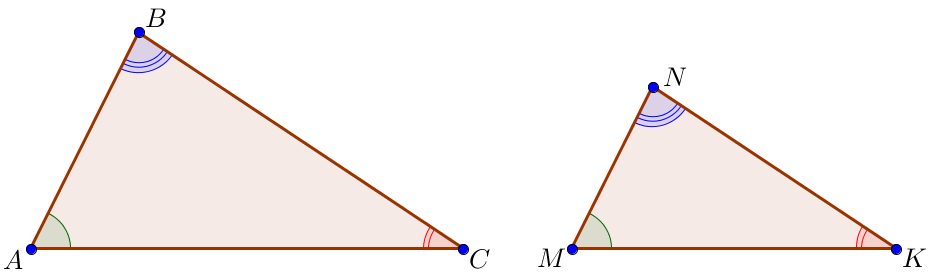
Решите задачу на готовом чертеже:
По данному рисунку найдите значение \(\displaystyle \color{red}{x}{\small.}\)
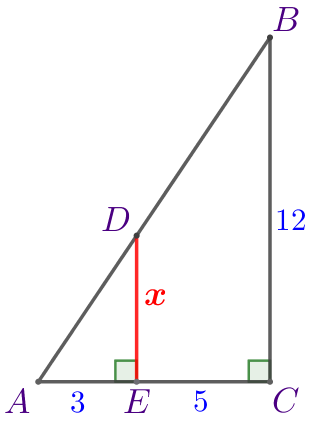
\(\displaystyle \color{red}{x}=\)\(\displaystyle {\small.}\)
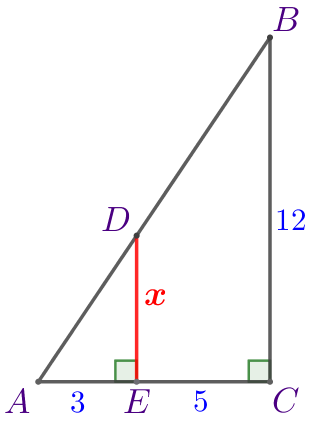 | \(\displaystyle ABC\) – треугольник:
Требуется найти значение \(\displaystyle \color{red}{x}{\small.}\) |
\(\displaystyle AC=8{\small.}\)
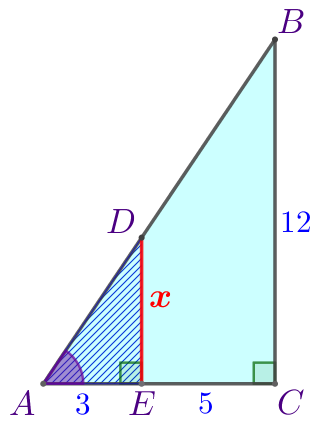
Рассмотрим треугольники \(\displaystyle ADE\) и \(\displaystyle ABC{\small:}\)
 |
|
Значит,
\(\displaystyle \triangle ADE \sim \triangle ABC\) по двум углам (по первому признаку подобия)
В подобных треугольниках напротив соответственно равных углов лежат сходственные стороны.
Следовательно,
\(\displaystyle \frac{DE}{BC}=\frac{AE}{AC}{\small.}\)
Подставим \(\displaystyle DE=\color{red}{x}{\small,}\) \(\displaystyle BC=12{\small,}\) \(\displaystyle AE=3{\small,}\) \(\displaystyle AC=8{\small:}\)
\(\displaystyle \frac{\color{red}{x}}{12}=\frac{3}{8}{\small.}\)
По свойству пропорции получаем:
\(\displaystyle \color{red}{x}=\frac{3 \cdot 12}{8}=\frac{36}{8}=\frac{9}{2}=4{,}5{\small.}\)
Ответ: \(\displaystyle \color{red}{x}=4{,}5{\small.}\)