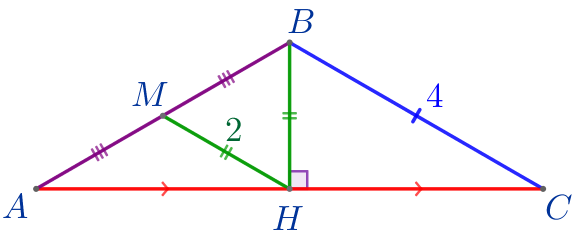
Найдите основание равнобедренного треугольника, если его боковая сторона равна \(\displaystyle 4\small,\) а высота, опущенная на основание, равна отрезку, соединяющему середину основания с серединой боковой стороны.
 | Введём обозначения: \(\displaystyle ABC\) – треугольник:
|
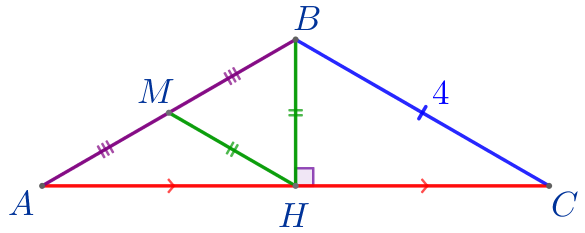
В равнобедренном треугольнике высота, проведенная к основанию, является медианой.
Значит, точка \(\displaystyle H\) – середина основания \(\displaystyle AC{\small:}\)
\(\displaystyle AH=CH=\frac{1}{2}AC{\small.}\)
\(\displaystyle MH=2{\small.}\)
По условию
\(\displaystyle BH=MH=2{\small.}\)
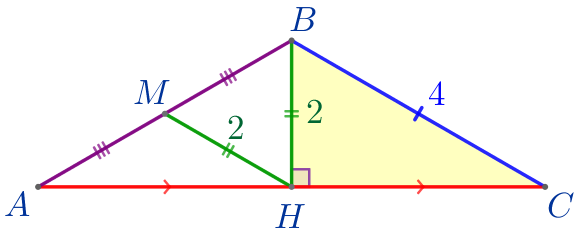 |
|
По теореме Пифагора сумма квадратов катетов равна квадрату гипотенузы:
\(\displaystyle BH^2+CH^2=BC^2{\small.}\)
Найдём \(\displaystyle CH{\small:}\)
\(\displaystyle CH^2=BC^2-BH^2{\small;}\)
\(\displaystyle CH^2=4^2-2^2=16-4=12{\small.}\)
Так как длина отрезка положительна, то
\(\displaystyle CH=2\sqrt{3}{\small.}\)
Найдём длину \(\displaystyle AC{\small.}\)
Так как \(\displaystyle CH=\frac{1}{2}AC{\small,}\) то
\(\displaystyle AC=2CH=2 \cdot 2\sqrt{3}=4\sqrt{3}{\small.}\)
Ответ: \(\displaystyle 4\sqrt{3}\small.\)