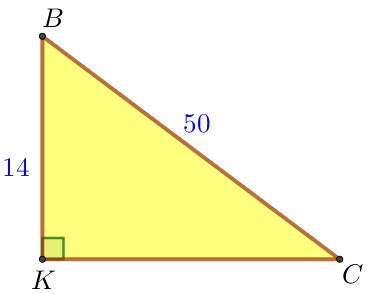
В равнобедренном треугольнике \(\displaystyle ABC\) медиана \(\displaystyle BK=14 {\small,}\) боковая сторона \(\displaystyle BC=50 {\small.}\) Найдите отрезок \(\displaystyle MN {\small,}\) если известно, что он соединяет середины боковых сторон.
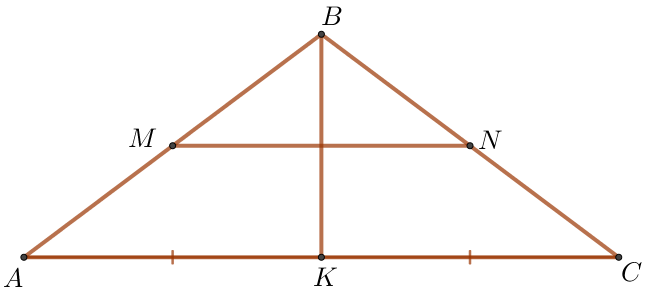
По условию отрезок \(\displaystyle MN\) соединяет середины боковых сторон треугольника \(\displaystyle ABC {\small.}\)
Значит, \(\displaystyle MN\) – средняя линия треугольника.
По правилу
Средняя линия треугольника параллельна стороне, против которой она лежит, и равна её половине.
получаем
\(\displaystyle MN=\frac{1}{2}\cdot AC {\small.}\)
По условию \(\displaystyle \triangle ABC\) – равнобедренный.
В равнобедренном треугольнике медиана, проведенная к основанию, является высотой.
Так как \(\displaystyle BK\) – медиана \(\displaystyle \triangle ABC{\small,}\) то
| 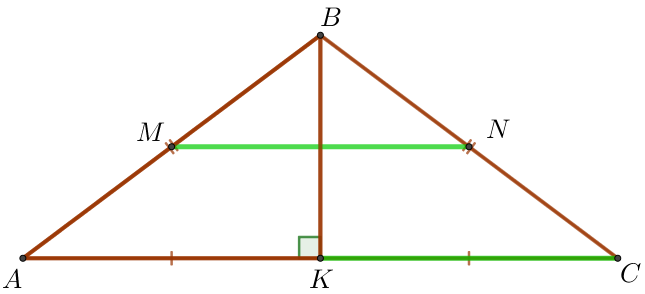 |
Следовательно,
\(\displaystyle MN=KC {\small.}\)
Рассмотрим прямоугольный треугольник \(\displaystyle BKC \small.\)
| По теореме Пифагора \(\displaystyle BC^2=KC^2+BK^2 {\small,}\) \(\displaystyle KC^2=BC^2-BK^2 {\small,}\) \(\displaystyle KC^2=50^2-14^2=2500-196=2304=48^2 {\small.}\) Так как длина отрезка положительна, то \(\displaystyle KC=48{\small.}\) |
Получаем
\(\displaystyle MN=KC=48 {\small.}\)
Ответ: \(\displaystyle 48 {\small.}\)