В прямоугольной трапеции \(\displaystyle ABCD\) с основаниями \(\displaystyle BC\) и \(\displaystyle AD\) угол \(\displaystyle BAD\) прямой, \(\displaystyle AB=12 {\small,}\) \(\displaystyle BC=CD=13 {\small.}\) Найдите среднюю линию трапеции.
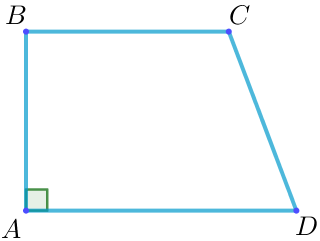
Тогда
\(\displaystyle \color{red}{l}=\frac{BC+AD}{2} {\small.}\)
Найдем длину отрезка \(\displaystyle AD {\small.}\)
Из точки \(\displaystyle C\) проведём высоту \(\displaystyle CH\) к стороне \(\displaystyle AD {\small.}\)
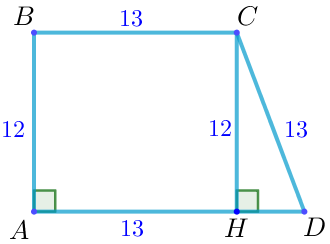 | Рассмотрим четырёхугольник \(\displaystyle ABCH {\small:}\)
Следовательно, \(\displaystyle ABCH \) – прямоугольник. Значит, \(\displaystyle AH=BC=13 {\small,}\) \(\displaystyle CH=AB=12 {\small.}\) |
Рассмотрим прямоугольный треугольник \(\displaystyle CDH {\small.}\) По теореме Пифагора \(\displaystyle CD^2=CH^2+HD^2 {\small,}\) \(\displaystyle HD^2=CD^2-CH^2 {\small,}\) \(\displaystyle HD^2=13^2-12^2=169-144=25=5^2 {\small.}\) Так как длина отрезка положительна, то \(\displaystyle HD=5{\small.}\) | 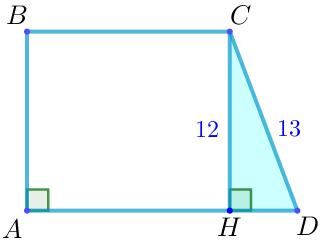 |
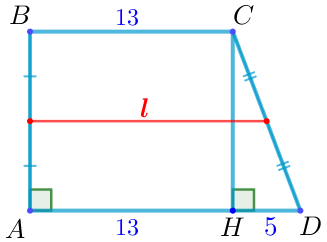 | Получаем \(\displaystyle AD=AH+HD=13+5=18 {\small.}\) Значит, \(\displaystyle \color{red}{l}=\frac{BC+AD}{2}=\frac{13+18}{2}=\frac{31}{2} =15{,}5 {\small.}\) |
Ответ: \(\displaystyle 15{,}5 {\small.}\)