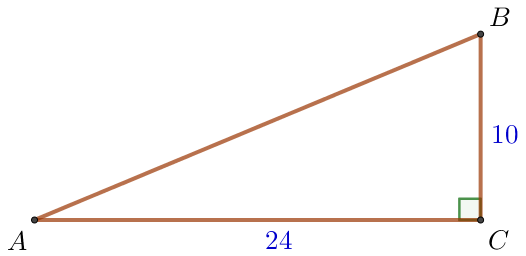
Катеты прямоугольного треугольника равны \(\displaystyle 10\) и \(\displaystyle 24 {\small.}\) Найдите наибольшую среднюю линию треугольника.
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Средняя линия треугольника параллельна стороне, против которой она лежит, и равна её половине.
Бóльшая средняя линия лежит напротив бóльшей стороны треугольника.
В прямоугольном треугольнике гипотенуза – бóльшая сторона.
Пусть \(\displaystyle ABC\) – прямоугольный треугольник с катетами \(\displaystyle AC=24 {\small,}\)\(\displaystyle BC=10 \) и гипотенузой \(\displaystyle AB {\small.}\)
По теореме Пифагора \(\displaystyle AB^2=AC^2+BC^2 {\small,}\) \(\displaystyle AB^2=24^2+10^2=576+100=676=26^2 {\small.}\) Так как длина отрезка положительна, то \(\displaystyle AB=26 {\small.}\) |
|
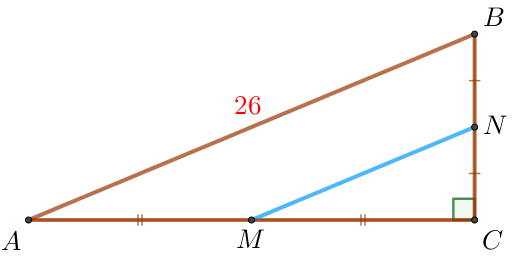 |
Пусть \(\displaystyle MN\) – бóльшая средняя линия треугольника \(\displaystyle ABC {\small,}\) тогда \(\displaystyle MN=\frac{1}{2} \cdot AB {\small,}\) \(\displaystyle MN=\frac{1}{2} \cdot 26=13{\small.}\) |
Ответ: \(\displaystyle 13 {\small.}\)