В параллелограмме диагонали являются биссектрисами его углов и равны \(\displaystyle 80\) и \(\displaystyle 84 {\small.}\) Найдите периметр параллелограмма.
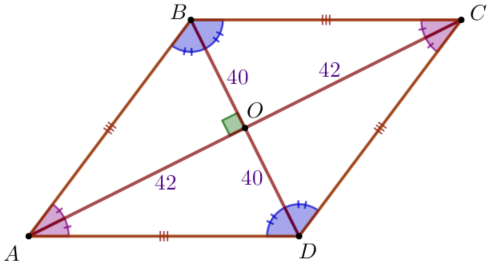
Пусть \(\displaystyle ABCD\) – параллелограмм с диагоналями \(\displaystyle AC=84\) и \(\displaystyle BD=80 {\small,}\) \(\displaystyle \\ O\) – точка пересечения диагоналей.
По условию диагонали данного параллелограмма являются биссектрисами.
Если у параллелограмма диагональ является биссектрисой его угла, то этот параллелограмм является ромбом.
Значит, \(\displaystyle ABCD\) – ромб. Тогда
|  |
Требуется найти периметр \(\displaystyle P_{ABCD}\) ромба. Так как стороны ромба равны, то
\(\displaystyle P_{ABCD}=4 \cdot AB {\small.}\)
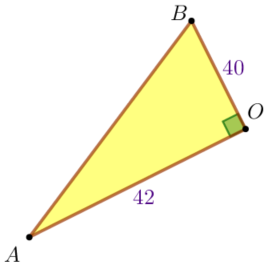 | Рассмотрим прямоугольный треугольник \(\displaystyle ABO {\small.}\) По теореме Пифагора \(\displaystyle AB^2=AO^2+BO^2 {\small,}\) \(\displaystyle AB^2=42^2+40^2 =1764+1600=3364=58^2{\small.}\) Так как длина отрезка положительна, то \(\displaystyle AB>0 {\small.}\) \(\displaystyle AB=58 {\small.}\) |
Получаем
\(\displaystyle P_{ABCD}=4 \cdot AB = 4 \cdot 58= 232 {\small.}\)
Ответ: \(\displaystyle 232 {\small. }\)