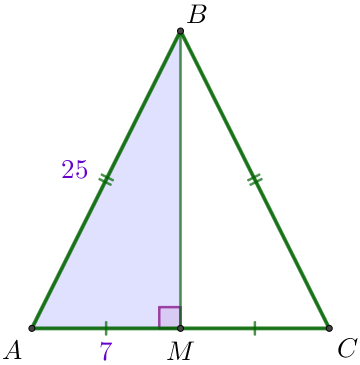
В треугольнике \(\displaystyle ABC\) известно, что \(\displaystyle AB=BC=25{\small,} \) \(\displaystyle AC=14{\small.} \) Найдите длину медианы \(\displaystyle BM{\small.} \)
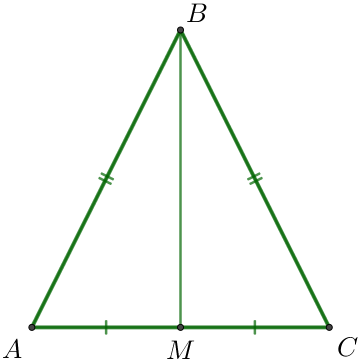
По условию \(\displaystyle AB=BC=25{\small,}\) то есть \(\displaystyle \triangle ABC\) – равнобедренный.
В равнобедренном треугольнике медиана, проведенная к основанию, является высотой.
Так как \(\displaystyle BM\) – медиана \(\displaystyle \triangle ABC\), то
| 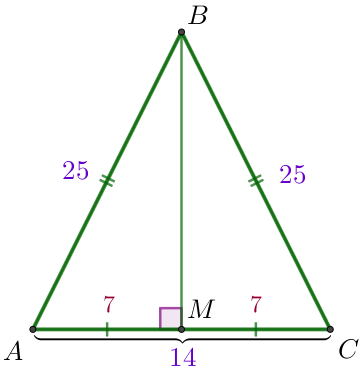 |
Рассмотрим прямоугольный треугольник \(\displaystyle ABM \small.\)
| По теореме Пифагора \(\displaystyle AB^2=AM^2+BM^2 {\small,}\) \(\displaystyle BM^2=AB^2-AM^2 {\small,}\) \(\displaystyle BM^2=25^2-7^2=625-49=576=24^2 {\small.}\) Так как длина отрезка положительна, то \(\displaystyle BM=24{\small.}\) |
Ответ: \(\displaystyle 24{\small.}\)