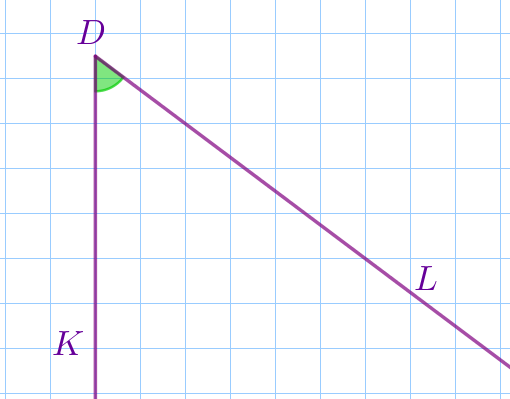
На клетчатой бумаге с размером клетки \(\displaystyle 1×1 \) изображён угол \(\displaystyle KDL{\small.}\) Найдите синус этого угла.
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе. | 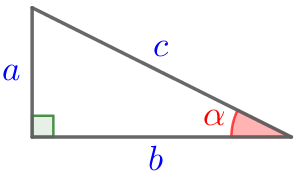 | \(\displaystyle \sin \alpha=\frac{a}{c}\) |
Построим прямоугольный треугольник с углом, равным углу \(\displaystyle D{\small.}\)
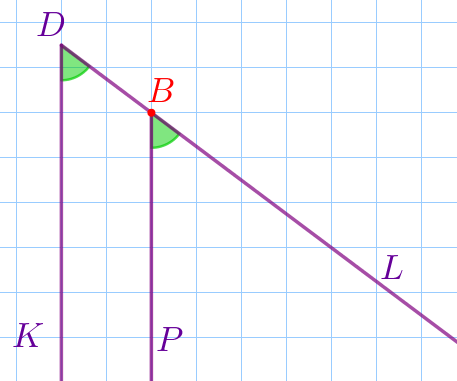 | На стороне \(\displaystyle DL\) угла \(\displaystyle KDL\) найдем точку, лежащую в узле квадратной сетки. Обозначим эту точку буквой \(\displaystyle B{\small.}\) Из точки \(\displaystyle B\) по линии сетки параллельно лучу \(\displaystyle DK\) проведём луч \(\displaystyle BP{\small.}\) \(\displaystyle \angle PBL=\angle KDL\) – соответственные углы при параллельных прямых \(\displaystyle BP\) и \(\displaystyle DK\) и секущей \(\displaystyle DL{\small.}\) |
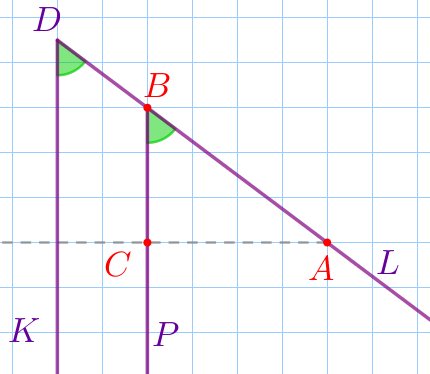 | На стороне \(\displaystyle BL\) угла \(\displaystyle PBL\) найдем точку, лежащую в узле квадратной сетки. Обозначим эту точку буквой \(\displaystyle A{\small.}\) Из точки \(\displaystyle A\) по линии сетки проведём перпендикуляр к стороне \(\displaystyle BP{\small.}\) Точку пересечения этого перпендикуляра и луча \(\displaystyle BP\) обозначим буквой \(\displaystyle C{\small.}\) Получили прямоугольный треугольник \(\displaystyle ABC{\small.}\) Катеты этого треугольника составляют целое количество клеток. |
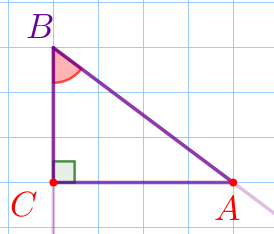
Рассмотрим прямоугольный треугольник \(\displaystyle ABC{\small.}\)
|
Значит, \(\displaystyle \sin \angle B = \frac{AC}{AB}{\small.}\) |
По рисунку определим длины катетов: \(\displaystyle BC=3{\small;}\) \(\displaystyle AC=4{\small.}\) По теореме Пифагора: \(\displaystyle AB^2=AC^2+BC^2{\small;}\) \(\displaystyle AB^2=4^2+3^2=16+9=25{\small.}\) Так как длина отрезка неотрицательна, то \(\displaystyle AB=\sqrt{25}=5{\small.}\) | 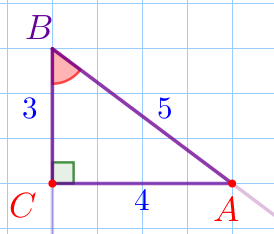 |
Тогда
\(\displaystyle \sin \angle B = \frac{AC}{AB}=\frac{4}{5}=0{,}8{\small.}\)
Ответ: \(\displaystyle \sin \angle KBL =0{,}8{\small.}\)