Задание
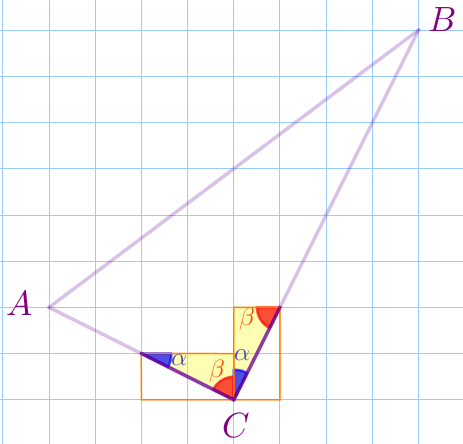
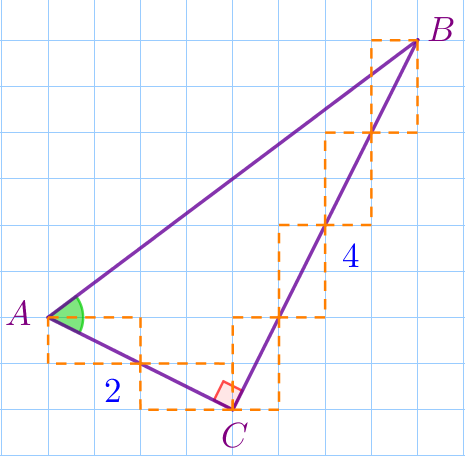
Найдите тангенс угла \(\displaystyle A\) треугольника \(\displaystyle ABC{\small,}\) изображенного на рисунке.
\(\displaystyle \tg \angle A=\)
Решение
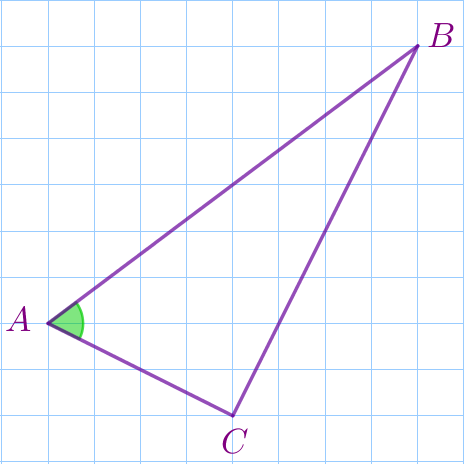
Рассмотрим треугольник \(\displaystyle ABC{\small.}\)
Заметим, что
\(\displaystyle \angle C=90^{\circ}{\small.}\)
Определение
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему. | 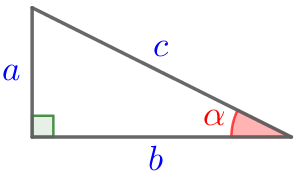 | \(\displaystyle \tg \alpha=\frac{a}{b}\) |
Рассмотрим прямоугольный треугольник \(\displaystyle ABC{\small:}\)
|
По рисунку определим длины катетов (в диагоналях прямоугольников размера \(\displaystyle 1×2{\small,}\) составленных из клеток квадратной решётки): \(\displaystyle BC=4{\small;}\) \(\displaystyle AC=2{\small.}\)
|
Тогда \(\displaystyle \tg \angle A = \frac{BC}{AC}=\frac{4}{2}=2{\small.}\) |
Ответ: \(\displaystyle \tg \angle A =2{\small.}\)