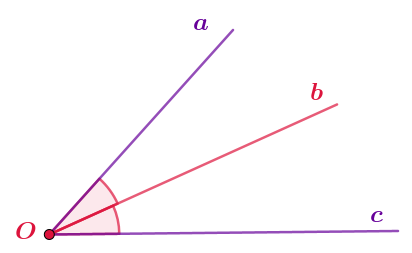
Три луча \(\displaystyle a{\small ,\;}b\) и \(\displaystyle c\) с общим началом \(\displaystyle O\) образуют углы величинами \(\displaystyle \alpha=74\degree \) и \(\displaystyle \beta=48\degree {\small .}\)
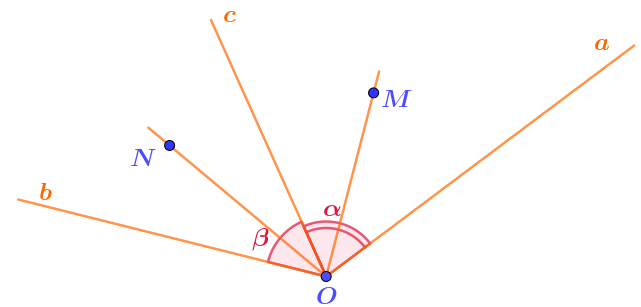
Проведены две биссектрисы этих углов \(\displaystyle OM\) и \(\displaystyle ON{\small .}\)
Сколько градусов составляет величина угла \(\displaystyle MON\,{\normalsize ?}\)
\(\displaystyle \angle MON=\)\(\displaystyle \degree \)
Искомый угол \(\displaystyle MON\) разделен лучом \(\displaystyle c\) на две части.
Значит, величина угла \(\displaystyle MON\) равна сумме величин этих углов. Найдем эти величины.
Равные углы имеют равные величины.
Значит,
- величина угла, образованного лучами \(\displaystyle ON\) и \(\displaystyle c{\small ,}\) равна половине величины угла \(\displaystyle bc{\small ,}\) то есть \(\displaystyle \frac{\beta}{2}{\small .}\)
- величина угла, образованного лучами \(\displaystyle OM\) и \(\displaystyle c{\small ,}\) равна \(\displaystyle \frac{\alpha}{2}\;-\)половине величины угла \(\displaystyle ac{\small .}\)
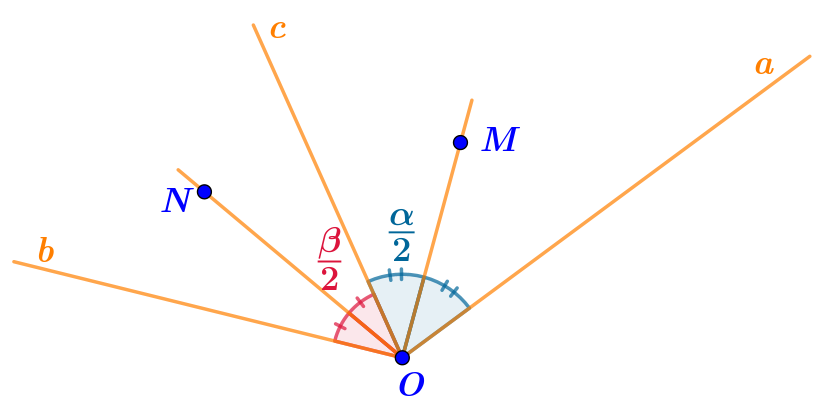
Величина составленного из частей угла равна сумме величин частей.
Значит,
\(\displaystyle \angle MON=\;\frac {\alpha}{2} + \frac {\beta}{2} \;=\;\frac {74\degree}{2} + \frac {48\degree}{2}=61\degree {\small .}\)
Ответ: \(\displaystyle \angle MON=61\degree {\small .}\)