Два угла имеют величины \(\displaystyle \alpha\) и \(\displaystyle \beta{\small .}\) При этом \(\displaystyle 90\degree >\alpha>\beta{\small .}\)
Равные им углы можно по-разному откладывать от луча \(\displaystyle OA{\small .}\)
Если откладывать углы в разные полуплоскости от продолжающей его прямой, то проведённые лучи образуют угол величиной \(\displaystyle 53\degree {\small .}\)
А если откладывать углы в одну сторону от этой прямой, то получится угол величиной \(\displaystyle 25\degree {\small .}\)
Найдите величины углов \(\displaystyle \alpha\) и \(\displaystyle \beta{\small .}\)
\(\displaystyle \alpha=\)\(\displaystyle \degree{\small ,\;} \;\;\;\;\beta=\)\(\displaystyle \degree\)
По условию задачи после откладывания углов дан угол между отложенными новыми лучами.
Отложим углы по одну сторону от прямой, продолжающей луч \(\displaystyle k{\small .} \)
На рисунке углы \(\displaystyle AOD \) и \(\displaystyle AOB \)располагаются по одну сторону прямой \(\displaystyle OA{\small .}\)
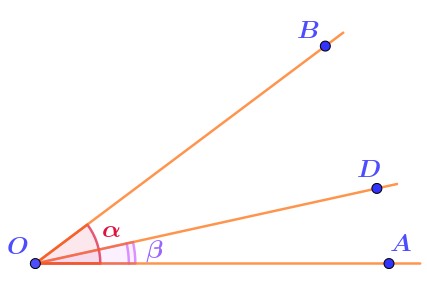
Тогда угол между проведенными лучами \(\displaystyle OD \) и \(\displaystyle OB \) равен \(\displaystyle 25\degree {\text :}\)
\(\displaystyle \angle BOD=25\degree{\small .} \)
Теперь отложим углы по разные стороны от прямой, продолжающей луч \(\displaystyle OA{\small .} \)
На рисунке угол \(\displaystyle AOD \) отложен по одну сторону прямой \(\displaystyle OA{\small ,}\) а угол \(\displaystyle AOC~-\) по другую.
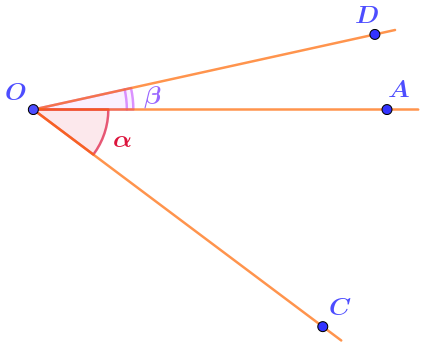
Тогда угол между проведенными лучами \(\displaystyle OC \) и \(\displaystyle OD \) равен \(\displaystyle 53\degree{\text :}\)
\(\displaystyle \angle COD=53\degree{\small .} \)
Объединяя в один рисунок, получаем:
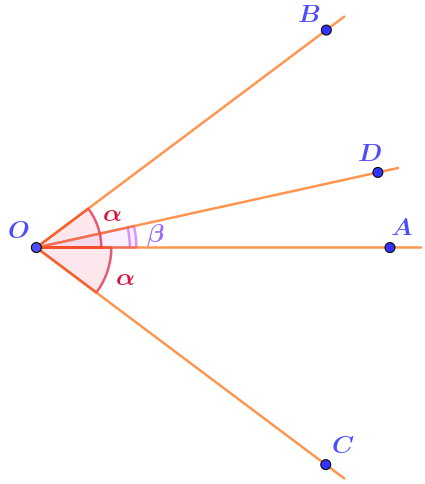
Величина угла \(\displaystyle BOC\) складывается из величин двух его частей:
\(\displaystyle \angle BOC=\angle COD+\angle BOD=53\degree +25\degree =78\degree {\small .}\)
С другой стороны, этот же угол получен двукратным откладыванием от луча \(\displaystyle OA\) угла величиной \(\displaystyle \alpha{\small .}\)
Значит,
\(\displaystyle \alpha=\frac{\angle BOC}{2}=\frac{78\degree }{2}=\)\(\displaystyle 39\degree {\small .}\)
Величина этого угла только что найдена и составляет \(\displaystyle 39\degree {\small .}\) Также известно, что величина угла \(\displaystyle BOD\) составляет \(\displaystyle 25\degree {\small .}\)
Угол \(\displaystyle AOB\) составлен из частей \(\displaystyle AOD\) и \(\displaystyle BOD{\small .}\)
Значит, величина угла \(\displaystyle AOD~-\) разность величин углов \(\displaystyle AOB\) и \(\displaystyle BOD{\text :}\)
\(\displaystyle \beta=\angle AOD=\angle AOB-\angle BOD=39\degree -25\degree =\)\(\displaystyle 14\degree {\small .}\)
Ответ: \(\displaystyle \alpha = 39\degree{\small ,}\)\(\displaystyle \beta = 14\degree {\small .}\)