Угол разделили на \(\displaystyle 6\) равных частей.
Затем тот же угол разделили на \(\displaystyle 9\) равных частей.
Сколько лучей для этого пришлось провести во внутренней области угла?
Обозначим через \(\displaystyle \alpha\) величину исходного угла.
Одну из сторон угла выберем для того, чтобы выразить величины углов, которые с этой стороной образуют проведённые лучи.
На рисунке эту сторону сделаем горизонтальной.
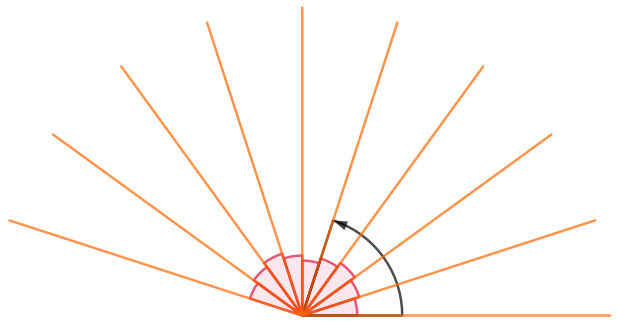
У равных углов равны величины.
Части \(\displaystyle -\) равные углы. Поэтому величина каждой из девяти частей равна \(\displaystyle \frac{\alpha}{9}{\small .}\)
Вычислим величины углов, образованных горизонтальным лучом и каждым из проведённых при делении.
Для этого последовательно умножим величину части на \(\displaystyle 1{\small ,\;}2{\small ,\;}3{\small ,\;}... {\small ,\;}8{\text :}\)
\(\displaystyle \frac{\alpha}{9}{\small ,\;\;\;\;}\frac{2\alpha}{9}{\small ,\;\;\;\;}\frac{3\alpha}{9}=\frac{\alpha}{3}{\small ,\;\;\;\;}\frac{4\alpha}{9}{\small ,\;\;\;\;}\frac{5\alpha}{9}{\small ,\;\;\;\;}\frac{6\alpha}{9}=\frac{2\alpha}{3}{\small ,\;\;\;\;}\frac{7\alpha}{9}{\small ,\;\;\;\;}\frac{8\alpha}{9}{\small .}\)

Части \(\displaystyle -\) равные углы. Поэтому величина каждой из шести частей равна \(\displaystyle \frac{\alpha}{6}{\small .}\)
Вычислим величины углов, образованных горизонтальным лучом и каждым из проведённых при делении.
Для этого последовательно умножим величину части на \(\displaystyle 1{\small ,\;}2{\small ,\;}3{\small ,\;}4{\small ,\;}5{\text :}\)
\(\displaystyle \frac{\alpha}{6}{\small ,\;\;\;\;}\frac{2\alpha}{6}=\)\(\displaystyle \frac{\alpha}{3}{\small ,\;\;\;\;}\)\(\displaystyle \frac{3\alpha}{6}=\frac{\alpha}{2}{\small ,\;\;\;\;}\frac{4\alpha}{6}=\)\(\displaystyle \frac{2\alpha}{3}{\small ,\;\;\;\;}\)\(\displaystyle \frac{5\alpha}{6}{\small .}\)
Видим, что два луча деления на \(\displaystyle 6\) частей образуют с горизонтальной стороной исходного угла углы ранее найденных величин.
Это величины углов, образованных лучами деления на \(\displaystyle 9\) частей с той же стороной исходного угла.
В одну сторону от луча можно единственным образом отложить угол данной величины.
Значит, углы повторяющихся величин являются просто одним углом.
После удаления повторений останется \(\displaystyle 11\) величин углов, которые лучи образуют с одной из сторон исходного угла:
\(\displaystyle \frac{\alpha}{9}{\small ,\;\;\;\;\;}\)\(\displaystyle \frac{\alpha}{6}{\small ,\;\;\;\;\;}\)\(\displaystyle \frac{2\alpha}{9}{\small ,\;\;\;\;\;}\)\(\displaystyle \frac{\alpha}{3}{\small ,\;\;\;\;\;}\)\(\displaystyle \frac{4\alpha}{9}{\small ,\;\;\;\;\;}\)\(\displaystyle \frac{\alpha}{2}{\small ,\;\;\;\;\;}\)\(\displaystyle \frac{5\alpha}{9}{\small ,\;\;\;\;\;}\)\(\displaystyle \frac{2\alpha}{3}{\small ,\;\;\;\;\;}\)\(\displaystyle \frac{7\alpha}{9}{\small ,\;\;\;\;\;}\)\(\displaystyle \frac{5\alpha}{6}{\small ,\;\;\;\;\;}\)\(\displaystyle \frac{8\alpha}{9}{\small .}\)
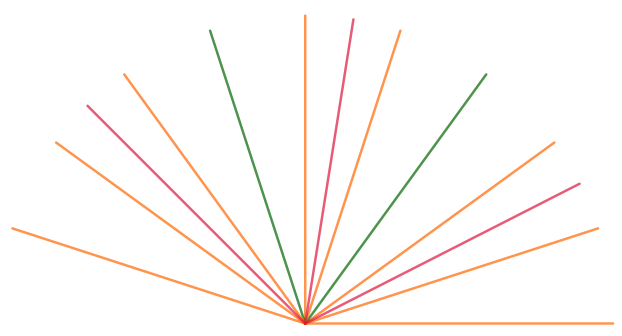
Ответ: \(\displaystyle 11\) лучей.