Проведено четыре разных луча с общим началом.
Первый и второй лучи образуют угол величиной \(\displaystyle 140\degree {\small .}\)
Равный этому угол образуют также второй и третий лучи, а ещё третий и четвёртый.
Найдите величину угла, образованного первым и четвёртым лучами.
\(\displaystyle \degree \)
Будем три раза подряд откладывать угол величиной \(\displaystyle 140\degree {\small .}\)
Начнём с первого луча, который изобразим горизонтально.
Учитывая условие, что все лучи разные, каждый раз угол будем откладывать в одном направлении. Например, против часовой стрелки.
При этом не получится, как могло бы казаться, угол величиной \(\displaystyle 280\degree{\small ,}\) поскольку величина угла не превышает \(\displaystyle 180^\circ{ \small .}\)
Проявляя осторожность, будем откладывать угол в \(\displaystyle 140\degree \) небольшими частями по \(\displaystyle 10\degree {\small .}\)
Процесс откладывания двух углов по \(\displaystyle 140\degree{\small ,}\) таким образом, превратится в \(\displaystyle 28\) откладываний углов по \(\displaystyle 10\degree{\small .}\)

Величина угла, образованного первым и последним лучами, сначала растёт с шагом в \(\displaystyle 10\degree{\small .}\)
После восемнадцатого откладывания она достигает максимально возможного значения в \(\displaystyle 180\degree {\small .}\)
Затем начинает убывать с шагом в \(\displaystyle 10\degree\) и за оставшиеся \(\displaystyle 10\) откладываний доходит до значения \(\displaystyle 80\degree {\small .}\)
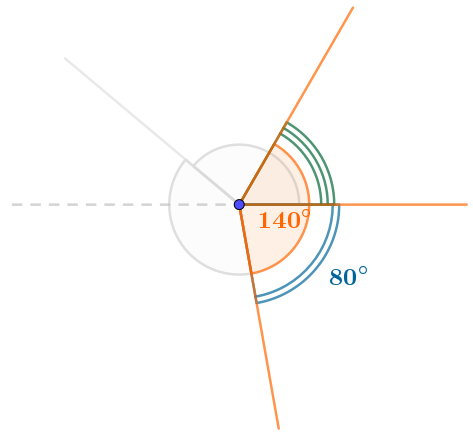
Тогда искомый угол становится частью угла угла величиной \(\displaystyle 140\degree {\small ,}\) при том, что величина другой части равна \(\displaystyle 80\degree {\small .}\)
Находим величину этого угла вычитанием:
\(\displaystyle 140\degree -80\degree=60\degree {\small .}\)
Обратим внимание: откладывая друг за другом углы по \(\displaystyle 10\degree{\small ,}\) мы должны повторить это действие \(\displaystyle 42\) раза. Тогда будут отложены все три угла по \(\displaystyle 140\degree {\small .}\)
За \(\displaystyle 18\) откладываний мы соберём по частям развёрнутый угол, за следующие \(\displaystyle 18\) раз \(\displaystyle -\) ещё один.
При этом мы, сделав полный оборот, вернёмся к первому лучу.
Останется ещё шесть откладываний, за которые набирается угол величиной \(\displaystyle 60\degree {\small .}\)
Ответ: \(\displaystyle 60\degree{\small .} \)