Проведена биссектриса \(\displaystyle FK\) угла \(\displaystyle AFB{\small .}\)
Затем проведена биссектриса \(\displaystyle FL\) угла \(\displaystyle AFK{\small .}\)
Наконец, проведена биссектриса \(\displaystyle FM\) угла \(\displaystyle BFL{\small .}\)
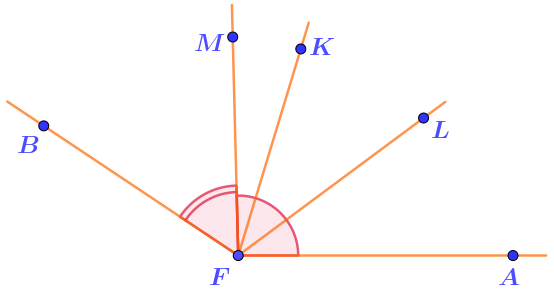
Найти отношение величин углов \(\displaystyle AFM\) и \(\displaystyle BFM{\small .}\)
\(\displaystyle \angle AFM : \angle BFM=\)\(\displaystyle :\)
Чтобы найти отношение величин углов \(\displaystyle AFM\) и \(\displaystyle BFM{\small ,}\) выразим величины этих углов через величину угла \(\displaystyle AFB{\small .}\)
Обозначим её через \(\displaystyle \alpha{\small .}\)
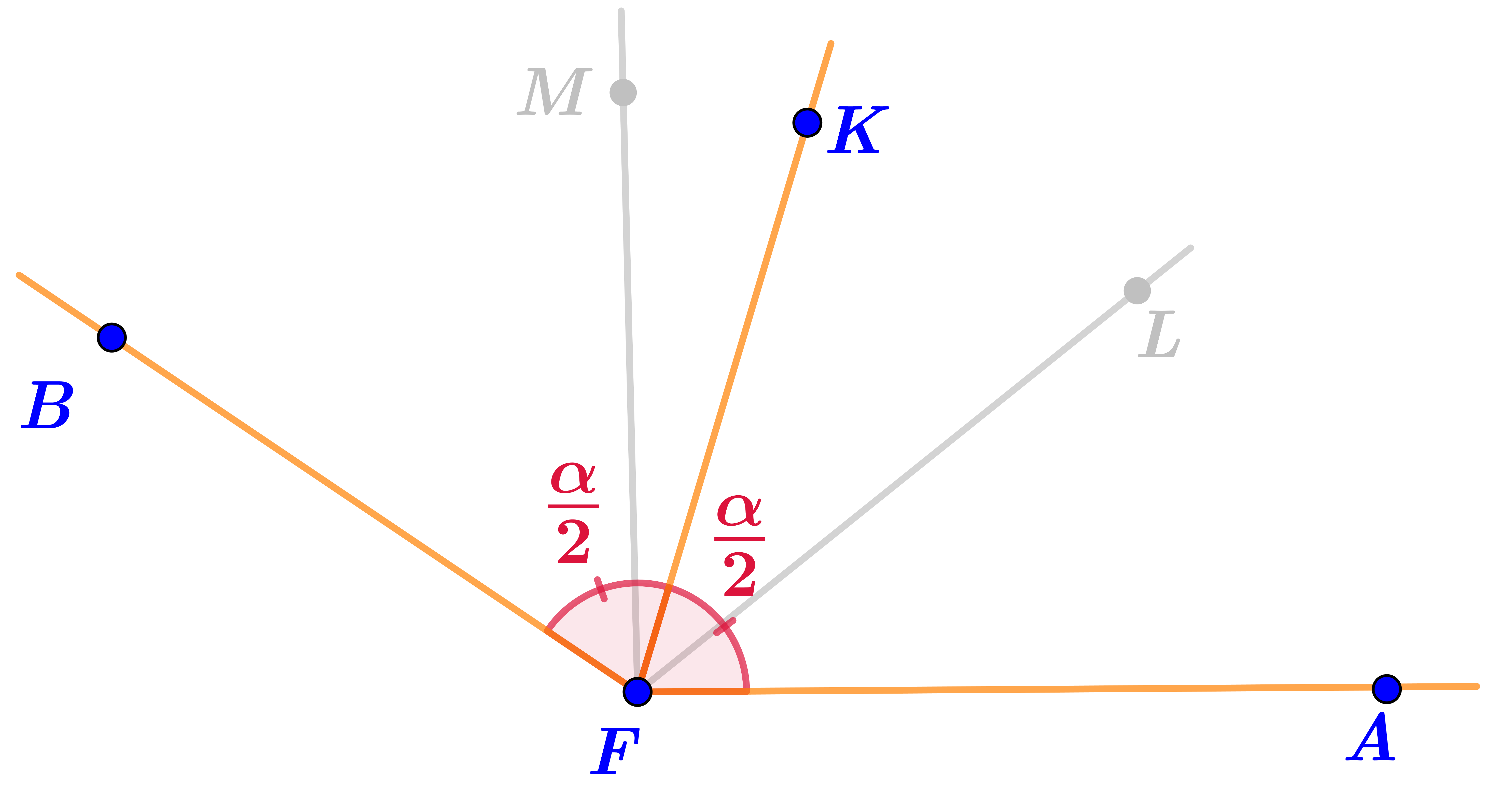
\(\displaystyle \angle BFK=\angle KFA=\frac {\alpha}{2}{\small .}\)
\(\displaystyle \angle KFL=\angle LFA=\frac{1}{2}\cdot \angle KFA=\frac{1}{2}\cdot\frac {\alpha}{2}=\frac {\alpha}{4}{\small .}\)
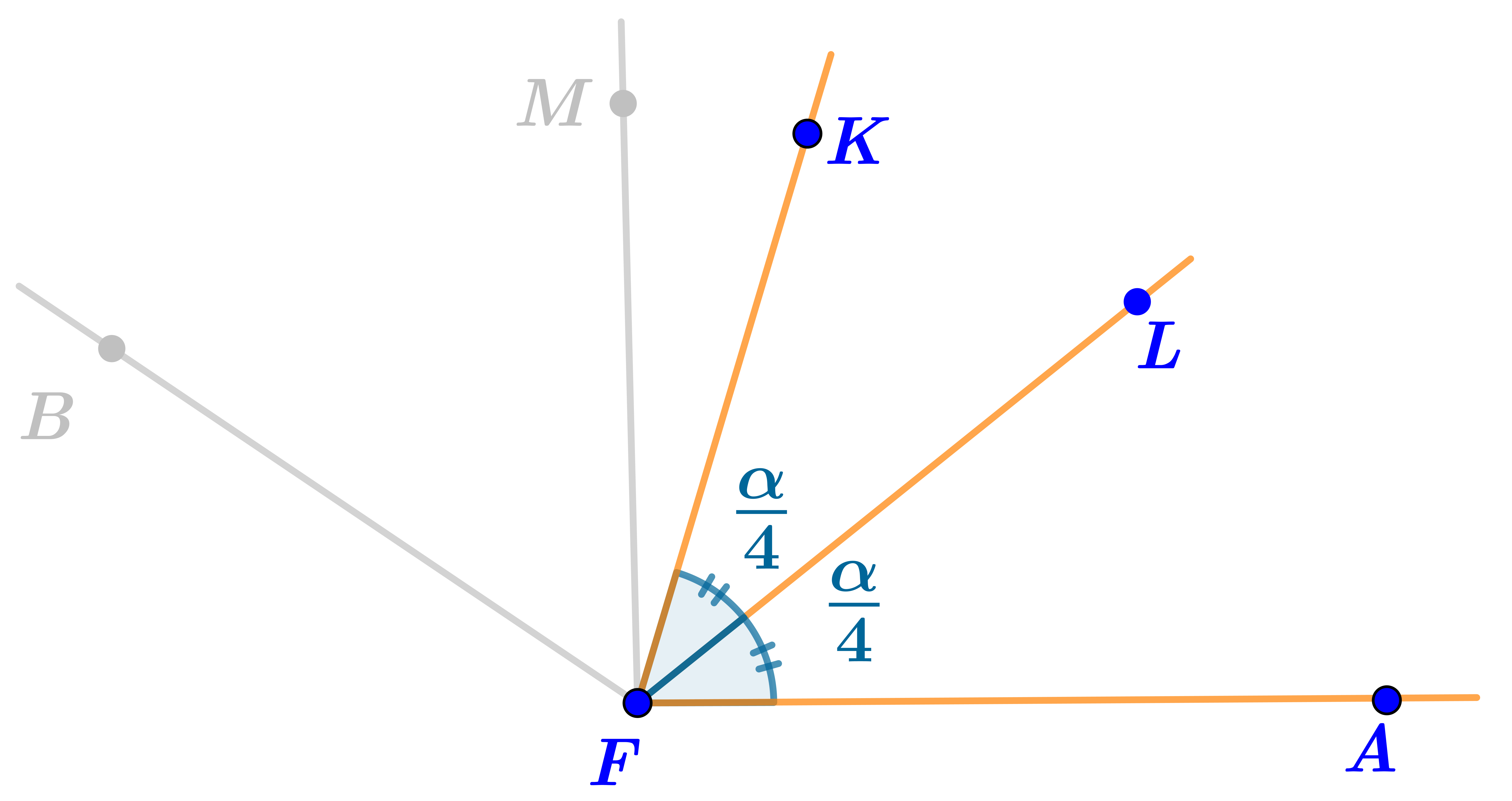
Вычтем из величины угла \(\displaystyle AFB\) величину его части \(\displaystyle LFA{\text :}\)
\(\displaystyle \angle BFL = \angle AFB-\angle LFA=\alpha-\frac {\alpha}{4}=\frac {3\alpha}{4}{\small .}\)
\(\displaystyle \angle BFM=\angle MFL=\frac{1}{2}\cdot\angle BFL=\frac{1}{2}\cdot\frac {3\alpha}{4}=\frac {3\alpha}{8}{\small .}\)
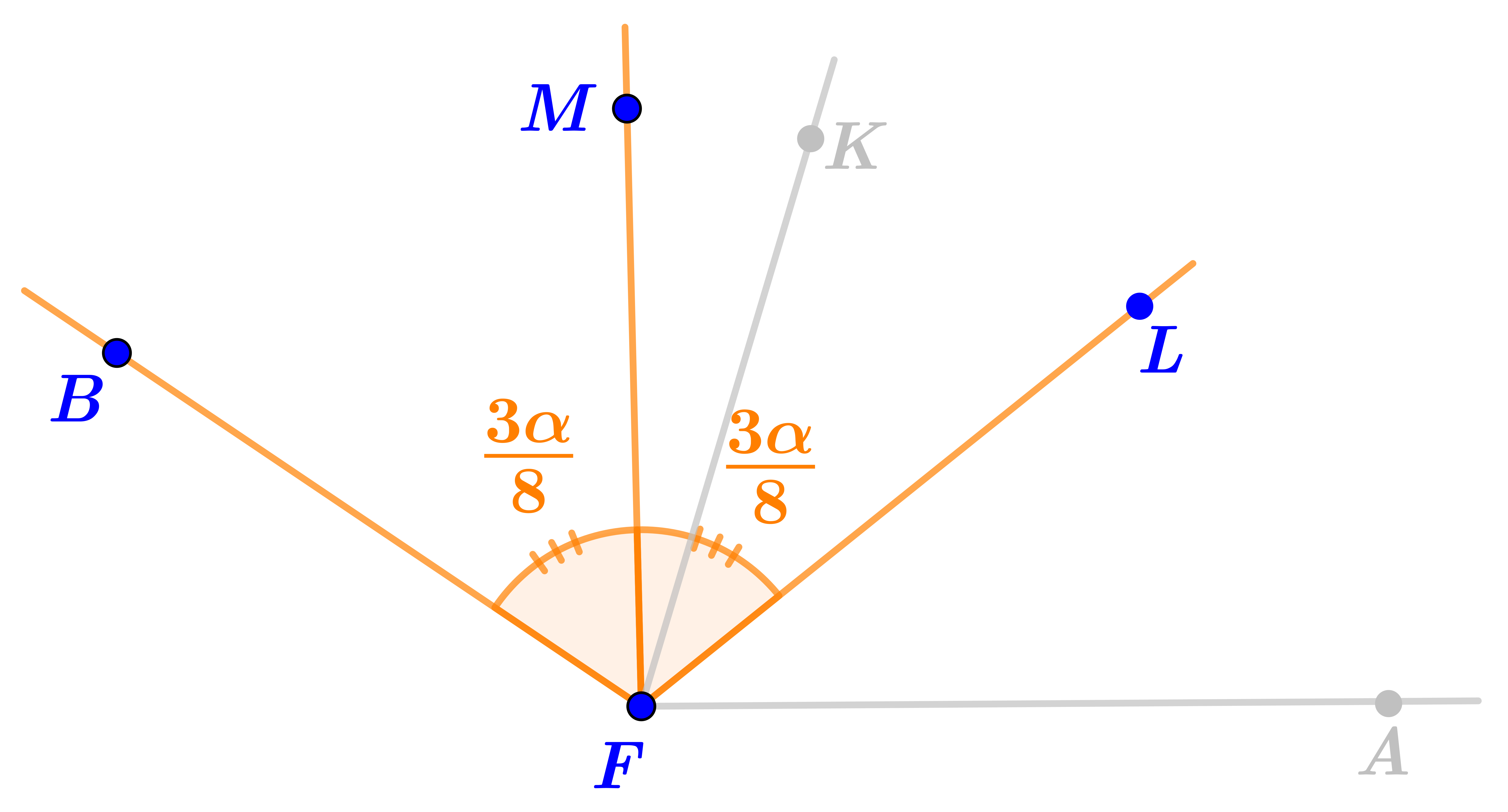
\(\displaystyle \angle AFM=\frac {3\alpha}{8}+\frac {\alpha}{4}=\frac {5\alpha}{8}{\small .}\)
\(\displaystyle \frac{\angle AFM}{\angle BFM} =\frac {5\alpha}{8} :\frac {3\alpha}{8}=\frac {5\alpha}{8} \cdot\frac {8}{3\alpha}=\frac {5}{3}{\small .}\)
Ответ: \(\displaystyle \angle AFM : \angle BFM=5:3{\small .}\)