На стороне \(\displaystyle AE\) треугольника \(\displaystyle AOE\) отмечены точки \(\displaystyle B{\small ,\;}C\) и \(\displaystyle D{\small .}\)
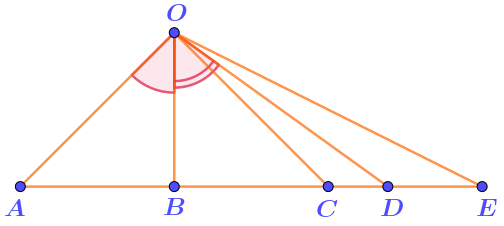
Лучи \(\displaystyle OB\) и \(\displaystyle OD\) являются биссектрисами углов\(\displaystyle AOC\) и \(\displaystyle COE\) и составляют угол величиной \(\displaystyle 46\degree {\small .}\)
Величина угла \(\displaystyle AOB\) равна \(\displaystyle 40\degree {\small .}\)
Найти величину угла \(\displaystyle DOE{\small .}\)
\(\displaystyle \angle DOE=\)\(\displaystyle \degree \)
Последовательно найдём углы, образованные лучами с общим началом в точке \(\displaystyle O{\small .}\)
Так что величина угла \(\displaystyle COB\) известна:
\(\displaystyle \angle COB=\angle AOB=40\degree {\small .}\)
Поскольку величина угла \(\displaystyle BOD\) складывается из величин его частей, можем найти величину угла \(\displaystyle COD\) вычитанием:
\(\displaystyle \angle COD=\angle BOD -\angle COB=46\degree -40\degree =6\degree {\small .}\)
\(\displaystyle \angle DOE=\angle COD=6\degree {\small .}\)
Ответ:\(\displaystyle 6\degree {\small .}\)